题目内容
12.在三棱锥PABC中,PA=BC=4,PB=AC=5,PC=AB=$\sqrt{11}$,则三棱锥PABC的外接球的表面积为( )| A. | 26π | B. | 12π | C. | 8π | D. | 24π |
分析 构造长方体,使得面上的对角线长分别为4,5,$\sqrt{11}$,则长方体的对角线长等于三棱锥P-ABC外接球的直径,即可求出三棱锥P-ABC外接球的表面积.
解答 解:∵三棱锥P-ABC中,PA=BC=4,PB=AC=5,PC=AB=$\sqrt{11}$,
∴构造长方体,使得面上的对角线长分别为4,5,$\sqrt{11}$,
则长方体的对角线长等于三棱锥P-ABC外接球的直径.
设长方体的棱长分别为x,y,z,则x2+y2=16,y2+z2=25,x2+z2=11,
∴x2+y2+z2=26,
∴三棱锥P-ABC外接球的直径为$\sqrt{26}$,
∴三棱锥P-ABC外接球的表面积为4π($\frac{\sqrt{26}}{2}$)2=26π.
故选:A.
点评 本题考查球内接多面体,考查学生的计算能力,构造长方体,利用长方体的对角线长等于四面体外接球的直径是关键.

练习册系列答案
相关题目
2.设M是椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上的一点,F1,F2为焦点,且$∠{F_1}M{F_2}=\frac{π}{3}$,则△MF1F2的面积为( )
| A. | 3 | B. | $16(2+\sqrt{3})$ | C. | $16(2-\sqrt{3})$ | D. | $3\sqrt{3}$ |
7.过坐标原点O的直线l与圆C:(x+1)2+(y-$\sqrt{3}$)2=100相交于A,B两点,当△ABO的面积最大时,则直线l的斜率是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
17.函数$f(x)=\frac{1}{2}{x^2}-lnx$的单调减区间( )
| A. | (-1,1] | B. | (0,1] | C. | (1,+∞) | D. | (0,+∞) |
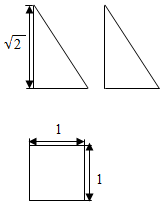 某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.
某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.