题目内容
三条直线l1:2x-y-10=0,l2:4x+3y-10=0,l3:ax+2y-8=0
(1)求l1与l2的夹角大小.(用反三角函数表示)
(2)若三条直线l1,l2,l3不能围成一个三角形,求a的所有可能值.
(1)求l1与l2的夹角大小.(用反三角函数表示)
(2)若三条直线l1,l2,l3不能围成一个三角形,求a的所有可能值.
考点:两直线的夹角与到角问题,直线的一般式方程
专题:
分析:(1)由夹角公式可得tanθ=|
|=2,由反三角函数可得;
(2)直线平行和直线共点即是不能围成三角形的情形.
2-(-
| ||
1+2×(-
|
(2)直线平行和直线共点即是不能围成三角形的情形.
解答:
解:(1)设l1与l2的夹角为θ,
∵l1:2x-y-10=0,l2:4x+3y-10=0,
∴两直线的斜率分别为2和-
,
∴由夹角公式可得tanθ=|
|=2,
∴l1与l2的夹角为arctan2;
(2)当l1与l3的平行(或重合)时可得-a-2×2=0,解得a=-4;
当l2与l3的平行(或重合)时可得3a-4×2=0,解得a=
;
当l1与l2与l3三线共点时,联立
可解得
,
代入l3的方程可得4a-4-8=0,解得a=3,
综上可得:a=-4或a=
或a=3
∵l1:2x-y-10=0,l2:4x+3y-10=0,
∴两直线的斜率分别为2和-
| 4 |
| 3 |
∴由夹角公式可得tanθ=|
2-(-
| ||
1+2×(-
|
∴l1与l2的夹角为arctan2;
(2)当l1与l3的平行(或重合)时可得-a-2×2=0,解得a=-4;
当l2与l3的平行(或重合)时可得3a-4×2=0,解得a=
| 8 |
| 3 |
当l1与l2与l3三线共点时,联立
|
|
代入l3的方程可得4a-4-8=0,解得a=3,
综上可得:a=-4或a=
| 8 |
| 3 |
点评:本题考查两直线的夹角问题,涉及直线平行关系的判断,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知线段AB、BD在平面α内,∠ABD=120°,线段AC⊥α,如果AB=a,BD=b,AC=c,则线段CD的长为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
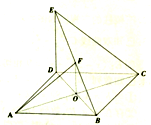 如图,菱形ABCD的边长为2,对角线交于点O,DE⊥平面ABCD;
如图,菱形ABCD的边长为2,对角线交于点O,DE⊥平面ABCD;