题目内容
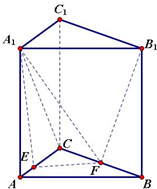 如图在三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,求几何体EFC-A1B1C1的体积.
如图在三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,求几何体EFC-A1B1C1的体积.考点:组合几何体的面积、体积问题
专题:计算题,空间位置关系与距离
分析:所求几何体的体积,转化为两个棱锥的体积之和,求解即可,
解答:
 解:所求几何体EFC-A1B1C1的体积,转化为两个棱锥A1-CEF和A1-BCC1B1的体积之和,∵三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,
解:所求几何体EFC-A1B1C1的体积,转化为两个棱锥A1-CEF和A1-BCC1B1的体积之和,∵三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,
∴VA1-CEF=
×
CE•CF•AA1=
×
×3×2×4=4.
VA1-BCC1B1=
BC•CC1•A1C1=
×4×4×4=
.
∴几何体EFC-A1B1C1的体积:4+
=
.
 解:所求几何体EFC-A1B1C1的体积,转化为两个棱锥A1-CEF和A1-BCC1B1的体积之和,∵三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,
解:所求几何体EFC-A1B1C1的体积,转化为两个棱锥A1-CEF和A1-BCC1B1的体积之和,∵三棱柱ABC-A1B1C1中,各侧棱都垂直于底面且地面为等腰直角三角形,∠ACB=90°,AC=BC=4,AA1=4,E,F分别在AC,BC上,且CE=3,CF=2,∴VA1-CEF=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
VA1-BCC1B1=
| 1 |
| 3 |
| 1 |
| 3 |
| 64 |
| 3 |
∴几何体EFC-A1B1C1的体积:4+
| 64 |
| 3 |
| 76 |
| 3 |
点评:本题考查几何体的体积的求法,转化思想的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
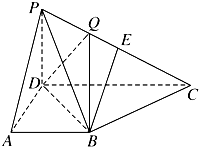 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为 如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.