题目内容
直线（c-d）（x-b）-（a-b）（y-d）=0与曲线（x-a）（x-b）-（y-c）（y-d）=0的交点个数是 ．
考点：两条直线的交点坐标,直线的一般式方程
专题：圆锥曲线的定义、性质与方程
分析：化简两个方程，根据直线与双曲线的位置关系可得结果．
解答：
解：∵曲线方程（x-a）（x-b）-（y-c）（y-d）=0
可化为，x2-y2-（a+b）x+（c+d）y+ab-cd=0，
∴曲线（x-a）（x-b）-（y-c）（y-d）=0是双曲线．
又∵直线方程（c-d）（x-b）-（a-b）（y-d）=0
可化为，
=
，
∴直线（c-d）（x-b）-（a-b）（y-d）=0过两点（a，c）和（b，d）．
∵点（a，c）和（b，d）也在双曲线（x-a）（x-b）-（y-c）（y-d）=0上，
∴由双曲线的性质可知，
直线（c-d）（x-b）-（a-b）（y-d）=0与曲线（x-a）（x-b）-（y-c）（y-d）=0有且仅有两个交点．
故答案为：2．
可化为，x2-y2-（a+b）x+（c+d）y+ab-cd=0，
∴曲线（x-a）（x-b）-（y-c）（y-d）=0是双曲线．
又∵直线方程（c-d）（x-b）-（a-b）（y-d）=0
可化为，
| x-b |
| a-b |
| y-d |
| c-d |
∴直线（c-d）（x-b）-（a-b）（y-d）=0过两点（a，c）和（b，d）．
∵点（a，c）和（b，d）也在双曲线（x-a）（x-b）-（y-c）（y-d）=0上，
∴由双曲线的性质可知，
直线（c-d）（x-b）-（a-b）（y-d）=0与曲线（x-a）（x-b）-（y-c）（y-d）=0有且仅有两个交点．
故答案为：2．
点评：本题考查两点式方程，双曲线的简单几何性质的综合应用．属于中档题．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
设函数f（x）的定义域为D，如果存在正实数k，对于任意x∈D，都有x+k∈D，且f（x+k）＞f（x）恒成立，则称函数f（x）为D上的“k型增函数”，已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x-a|-2a，若f（x）为R上的“2014型增函数”，则实数a的取值范围是（ ）
| A、a＜-1007 | ||
| B、a＜1007 | ||
C、a＜
| ||
D、a＜-
|
下列命题中正确的是（ ）
A、若
| ||||||||||||
B、向量
| ||||||||||||
| C、空间任意两个向量共面 | ||||||||||||
D、若
|
若不等式2x＞x2+a对于一切x∈[-2，3]恒成立，则实数a的取值范围（ ）
| A、（-∞，-8） |
| B、（-∞，-3） |
| C、（-∞，1） |
| D、（-8，-∞） |
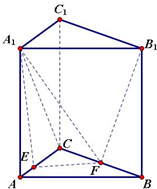如图在三棱柱ABC-A1B1C1中，各侧棱都垂直于底面且地面为等腰直角三角形，∠ACB=90°，AC=BC=4，AA1=4，E，F分别在AC，BC上，且CE=3，CF=2，求几何体EFC-A1B1C1的体积．