题目内容
13.过点$(5,\frac{9}{4})$作直线,使它与双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1有且只有一个公共点,这样的直线有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 利用几何法,结合双曲线的几何性质,得出符合条件的结论.
解答 解:∵点P点$(5,\frac{9}{4})$,x=5时,y=±$\frac{9}{4}$,显然点$(5,\frac{9}{4})$在双曲线上,过点$(5,\frac{9}{4})$作直线,与双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1有且只有一个公共点的直线有3条.
第1条是双曲线的切线,第2、3条是与两条渐近线平行的直线,
综上,符合条件的直线只有3条.
故选:C.
点评 本题考查了直线与双曲线的交点的问题,解题时应灵活应用双曲线的渐近线,是基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
9.已知点A(cos80°,sin80°),B(cos20°,sin20°),则|$\overrightarrow{AB}$|等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
8.当n=4时,执行如图所示的程序框图,输出S的值是( )


| A. | 7 | B. | 9 | C. | 11 | D. | 16 |
5.已知抛物线y2=2px(p>0)上一点M (x0,4)到焦点F 的距离|MF|=$\frac{5}{4}$x0,则直线 MF 的斜率kMF=( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
2.抛物线4y=x2的焦点到准线的距离为( )
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
3.已知a=log32,b=log2$\frac{1}{3}$,c=2${\;}^{\frac{1}{3}}$,则( )
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
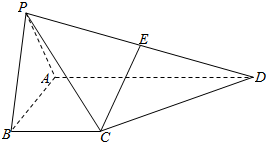 如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.
如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.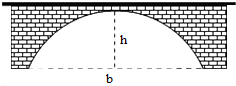 如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.
如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.