题目内容
5.已知抛物线y2=2px(p>0)上一点M (x0,4)到焦点F 的距离|MF|=$\frac{5}{4}$x0,则直线 MF 的斜率kMF=( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
分析 根据定义抛物线y2=2px(p>0)上一点M (x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0,求出x0,然后M (2p,4)代入y2=2px,可得p=2,即可求出直线MF的斜率.
解答 解:根据定义抛物线y2=2px(p>0)上一点M(x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0,
∴x0+$\frac{p}{2}$=$\frac{5}{4}$x0,x0=2p,
∴M(2p,4)代入y2=2px,可得p=2,
∴M(4,4),F(1,0),
∴kMF=$\frac{4-0}{4-1}$=$\frac{4}{3}$.
故选:B.
点评 本题考查了抛物线的定义和性质,解题的关键是根据定义得出M的坐标,属于基础题.

练习册系列答案
相关题目
16.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右顶点分别是A1、A2,线段A1A2被抛物线y2=bx的焦点分为3:1两段,则此双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{5}-1$ |
20.某程序框图如图所示,若该程序运行后输出的值是$\frac{23}{12}$,则a的值为( )
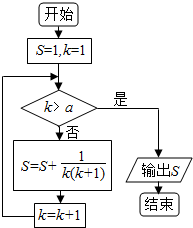

| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
10.执行如图所示的程序框图,则输出的s的值为( )


| A. | -7 | B. | -5 | C. | 2 | D. | 9 |
14.已知全集U={x∈N|x<6},集合A={1,3},B={3,5},则∁U(A∪B)=( )
| A. | {0,2,4} | B. | {2,4} | C. | {0,3,4} | D. | {3,4} |
