如图.一桥拱的形状为抛物线.此时水面距桥拱顶端h=6m.水面宽b=24m.若水面上升2m后.水面宽为8$\sqrt{6}$米．题目和参考答案——青夏教育精英家教网—

题目内容

18．

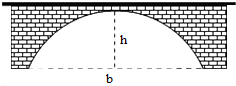如图，一桥拱的形状为抛物线，此时水面距桥拱顶端h=6m，水面宽b=24m，若水面上升2m后，水面宽为8$\sqrt{6}$米．

分析建立直角坐标系，设抛物线为y=ax²，把点（12，-6）代入求出解析式，根据当y=-4时，求出x的值，即可得出水面宽度．

解答解：如图，建立直角坐标系，
可设这条抛物线为y=ax²，
把点（12，-6）代入，得-6=a•12²，
解得a=-$\frac{1}{24}$，
∴y=-$\frac{1}{24}$x²，
当y=-4时，-4=-$\frac{1}{24}$x²，
解得x=±4$\sqrt{6}$，
∴水面上升2m，水面宽度为8$\sqrt{6}$m．
故答案为：8$\sqrt{6}$．

点评本题主要考查了抛物线的应用，根据已知建立坐标系从而得出抛物线解析式是解决问题的关键．

练习册系列答案

9．已知△ABC的三个内角A，B，C所对应的边分别为a，b，c，B=$\frac{π}{4}$，b=4，则ac的取值范围为（0，$8（2+\sqrt{2}）$]．

6．对于任意两个非零向量$\overrightarrow{α}$和$\overrightarrow{β}$，定义$\overrightarrow{α}$?$\overrightarrow{β}$=$\frac{\overrightarrow{α}•\overrightarrow{β}}{\overrightarrow{β}•\overrightarrow{β}}$，若两个非零的平面向量$\overrightarrow{α}$，$\overrightarrow{β}$满足|$\overrightarrow{α}$|≥|$\overrightarrow{β}$|，其夹角θ∈（0，$\frac{π}{4}$），且$\overrightarrow{α}$?$\overrightarrow{β}$和$\overrightarrow{β}$?$\overrightarrow{α}$都在集合$\left\{{\frac{n}{2}|n∈Z}\right\}$中，则$\overrightarrow{α}$?$\overrightarrow{β}$=（　　）

13．过点$（5，\frac{9}{4}）$作直线，使它与双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1有且只有一个公共点，这样的直线有（　　）

3．一个圆锥筒的底面半径为3cm，其母线长为5cm，则这个圆锥筒的体积为12πcm³．

10．执行如图所示的程序框图，则输出的s的值为（　　）

7．已知抛物线的顶点在原点，对称轴是x轴，直线y=2x-4截抛物线弦长|AB|=$3\sqrt{5}$，求抛物线标准方程及它的准线方程．

8．已知函数f（x）=e^x-e^-x，e为自然对数的底，则下列结论正确的是（　　）

	A．	f（x）为奇函数，且在R上单调递增		B．	f（x）为偶函数，且在R上单调递增
	C．	f（x）为奇函数，且在R上单调递减		D．	f（x）为偶函数，且在R上单调递减

试题分类