题目内容
13．已知函数f（x）=sin2x+$\frac{1}{2}$的最小正周期是（ ）| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
分析 利用降幂公式化简函数的解析式，再利用函数y=Asin（ωx+φ）的周期性，得出结论．
解答 解：函数f（x）=sin2x+$\frac{1}{2}$=$\frac{1-cos2x}{2}$+$\frac{1}{2}$=1-$\frac{1}{2}$cos2x 的最小正周期是$\frac{2π}{2}$=π，
故选：B．
点评 本题主要考查降幂公式，函数y=Asin（ωx+φ）的周期性，利用了函数y=Asin（ωx+φ）的周期为$\frac{2π}{ω}$，属于基础题．
练习册系列答案
相关题目
3．设函数f（x）=x2+ax+b2，若a是从区间[0，3]内任取的一个数，b是从区间[0，2]内任取的一个数，则f（x）的图象全在x轴上方的概率是（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{1}{6}$ | D． | $\frac{5}{6}$ |
4．过抛物线y2=2px（p＞0）的焦点F作直线交抛物线于A，B，若S△OAF=4S△OBF，则直线AB的斜率为（ ）
| A． | ±$\frac{3}{5}$ | B． | ±$\frac{4}{5}$ | C． | ±$\frac{3}{4}$ | D． | ±$\frac{4}{3}$ |
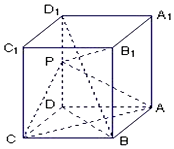如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P是DD1的中点．