题目内容
4.过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A,B,若S△OAF=4S△OBF,则直线AB的斜率为( )| A. | ±$\frac{3}{5}$ | B. | ±$\frac{4}{5}$ | C. | ±$\frac{3}{4}$ | D. | ±$\frac{4}{3}$ |
分析 据S△AOF=4S△BOF,得|AF|=4|BF|,$\overrightarrow{AF}=4\overrightarrow{FB}$,求得-y1=4y2,设出直线AB的方程,与抛物线方程联立消去x,利用韦达定理求出斜率,即可求出tanα.
解答 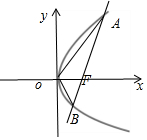 解:根据题意设点A(x1,y1),B(x2,y2).
解:根据题意设点A(x1,y1),B(x2,y2).
由S△AOF=4S△BOF,得|AF|=4|BF|,|,$\overrightarrow{AF}=4\overrightarrow{FB}$,得$(\frac{p}{2}-{x}_{1},-{y}_{1})=4({x}_{2}-\frac{p}{2},{y}_{2})$,
故-y1=4y2,即$\frac{{y}_{1}}{{y}_{2}}=-4$.
设直线AB的方程为y=k(x-$\frac{p}{2}$).联立$\left\{\begin{array}{l}{y=k(x-\frac{p}{2})}\\{{y}^{2}=2px}\end{array}\right.$,消元得ky2-2py-kp2=0.
故y1+y2=$\frac{2p}{k}$,y1y2=-p2.则$\frac{{(y}_{1}{+y}_{2})^{2}}{{y}_{1}{y}_{2}}=\frac{{y}_{1}}{{y}_{2}}+\frac{{y}_{2}}{{y}_{1}}+2=-\frac{9}{4}$,
$-\frac{4}{{k}^{2}}=-\frac{9}{4}$,解得k=$±\frac{4}{3}$,即直线AB的斜率为$±\frac{4}{3}$.
故选:D.
点评 本题主要考查了抛物线的概念和性质,直线和抛物线的综合问题,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
15.已知双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),点F为E的左焦点,点P为E上位于第一象限内的点,P关于原点的对称点为Q,且满足|PF|=3|FQ|,若|OP|=b,则E的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
12.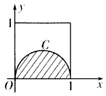 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )| A. | 157 | B. | 314 | C. | 486 | D. | 628 |
19.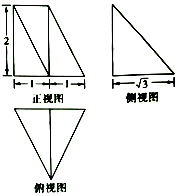 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$$\sqrt{3}$ | D. | $\frac{5}{3}$$\sqrt{3}$ |
9.已知函数$f(x)=ln({x+1})-\frac{ax}{1-x}({a∈R})$.
(1)当a=1时,求函数f(x)的单调区间;
(2)若-1<x<1时,均有f(x)≤0成立,求实数a的取值范围.
(1)当a=1时,求函数f(x)的单调区间;
(2)若-1<x<1时,均有f(x)≤0成立,求实数a的取值范围.
13.已知函数f(x)=sin2x+$\frac{1}{2}$的最小正周期是( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |