题目内容
2.若0<a<2,0<b<2,则函数$f(x)=\frac{1}{3}{x^3}+\sqrt{a}{x^2}+2bx-3$存在极值的概率为$\frac{1}{4}$.分析 求导,由函数存在极值,则f′(x)=0,存在两个不相等的实根,则△>0,求得a>2b,求得阴影部分的面积,利用几何概型概率公式,即可求得答案.
解答 解:由数$f(x)=\frac{1}{3}{x^3}+\sqrt{a}{x^2}+2bx-3$,求导,f′(x)=x2+2$\sqrt{a}$+2b,
由函数存在极值.则方程x2+2$\sqrt{a}$+2b=0,有两个不相等的实根,
△=4a-4×2b>0,即a>2b,
∴由题意可知阴影部分的面积S1=$\frac{1}{2}$×2×1=1,
a,b所围成图形的面积S=2×2=4,
∴存在极值的概率S=$\frac{{S}_{1}}{S}$=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题考查几何概型概率公式,极值存在的应用,考查计算能力,属于中档题.

练习册系列答案
相关题目
12.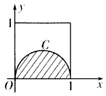 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )| A. | 157 | B. | 314 | C. | 486 | D. | 628 |
13.已知函数f(x)=sin2x+$\frac{1}{2}$的最小正周期是( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
17.双曲线mx2-y2=1(m∈R)与椭圆$\frac{x^2}{5}+{y^2}=1$有相同的焦点,则该双曲线的渐近线方程为( )
| A. | $y=±\sqrt{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | $y=±\frac{1}{3}x$ | D. | y=±3x |
7.在△ABC中,角A,B,C的对边分别为a,b,c,若c=2,a2=b2+1,则acosB=( )
| A. | $\frac{5}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | 5 |
12.经过双曲线的左焦点F1作倾斜角为30°的直线,与双曲线的右支交于点P,若以PF1为直径的圆恰好经过双曲线的右焦点,则双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |