题目内容
3.设函数f(x)=x2+ax+b2,若a是从区间[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,则f(x)的图象全在x轴上方的概率是( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
分析 本题考查的知识点是几何概型的意义,关键是要找出(a,b)对应图形的面积,及满足条件“f(x)的图象全在x轴上方”的点对应的图形的面积,然后再结合几何概型的计算公式进行求解.
解答 解:试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2},其面积为6.
构成事件“f(x)的图象全在x轴上方”的区域为{(a,b)|0≤a≤3,0≤b≤2,|a|<2|b|},面积为6-$\frac{1}{2}×3×1.5$=$\frac{15}{4}$.
所以所求的概率为=$\frac{\frac{15}{4}}{6}$=$\frac{5}{8}$.
故选:B
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
18.直线a、b和平面α,下面推论错误的是( )
| A. | 若a⊥α,b?α,则a⊥b | B. | 若a⊥α,a∥b,则b⊥α | ||
| C. | 若a⊥b,b⊥α,则a∥α或a?α | D. | 若a∥α,b?α,则a∥b |
15.已知双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),点F为E的左焦点,点P为E上位于第一象限内的点,P关于原点的对称点为Q,且满足|PF|=3|FQ|,若|OP|=b,则E的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
12.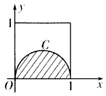 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )| A. | 157 | B. | 314 | C. | 486 | D. | 628 |
13.已知函数f(x)=sin2x+$\frac{1}{2}$的最小正周期是( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |

 已知函数f(x)=|2x-1|-2|x-1|.
已知函数f(x)=|2x-1|-2|x-1|.