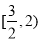题目内容
3.函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$与g(x)=$\frac{1}{2}$(|x+a|+1)的图象上存在关于y轴对称的点,则实数a的取值范围是( )| A. | (-∞,3-2ln2] | B. | [3-2ln2,+∞) | C. | [$\sqrt{e}$,+∞) | D. | (-∞,$-\sqrt{e}$] |
分析 画出函数f(x)的图象,求出函数g(x)=$\frac{1}{2}$(|x+a|+1)的最小值,利用已知条件转化列出不等式求解即可.
解答 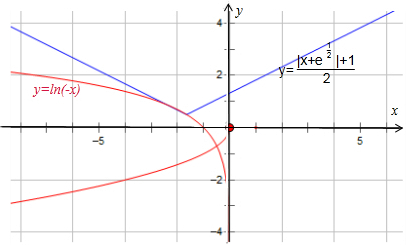 解:函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$的图象如图:
解:函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$的图象如图:
g(x)=$\frac{1}{2}$(|x+a|+1)$≥\frac{1}{2}$,当且仅当x=-a时取等号,
函数y=ln(-x)与y=$\frac{1}{2}$(|x+$\sqrt{e}$|+1)在x<0有解,而且g(x)=$\frac{1}{2}$(|x+a|+1)看作g(x)=$\frac{1}{2}$(|x|+1)向左平移而得,y′=[ln(-x)]′=$\frac{1}{x}$,可得切点横坐标为:$\frac{1}{x}=-\frac{1}{2}$,即x=-2,
此时a取得最小值:ln2=$\frac{1}{2}$(|-2+a|+1),解得a=3-2ln2.
函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$与g(x)=$\frac{1}{2}$(|x+a|+1)的图象上存在关于y轴对称的点,
所以实数a的取值范围是:[3-2ln2,+∞).
故选:B.
点评 本题考查函数的零点,函数的图象的画法,考查数形结合以及转化思想的应用.

练习册系列答案
相关题目
12.命题“存在x0∈R+,使log2x0≤0”的否定是( )
| A. | 不存在x0∈R+,使log2x0>0 | B. | 对任意的x∈R+,有log2x>0 | ||
| C. | 对任意的x∈R+,有log2x≤0 | D. | 存在x0∈R+,使log2x0>0 |

 B.4
B.4 C.4
C.4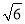 D.
D.
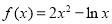 在其定义域的一个子区间
在其定义域的一个子区间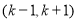 内不是单调函数,则实数
内不是单调函数,则实数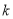 的取值范围是( )
的取值范围是( )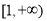 B.
B.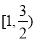 C.
C. D.
D.