Question

已知函数f（x）=|2x-1|．
（1）画出函数f（x）的图象，并写f（x）的单调增区间；
（2）解不等式|2x-1|＜3．

Answer 1

考点：绝对值不等式的解法

专题：不等式的解法及应用

分析：（1）化简函数f（x）=|2x-1|的解析式，画出f（x）的图象，数形结合求得f（x）的单调增区间．
（2）由不等式|2x-1|＜3，可得-3＜2x-1＜3，由此求得不等式的解集．

解答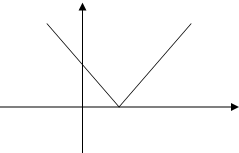： 解：（1）函数f（x）=|2x-1|=

2x-1，x≥ 1 2 1-2x，x＜ 1 2

，所以f（x）的图象如图所示：
结合函数的图象可得，f（x）的单调增区间为[

1

2

，+∞）．
（2）由不等式|2x-1|＜3，可得-3＜2x-1＜3，求得-1＜x＜2，
故不等式的解集为（-1，2）．

点评：本题主要考查带有绝对值的函数，绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．