题目内容
已知命题p:在x∈[1,2]时,不等式x2+ax-2>0恒成立;命题q:函数f(x)=log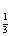 (x2-2ax+3a)是区间[1,+∞)上的减函数.若命题“p∨q”是真命题,求实数a的取值范围.
(x2-2ax+3a)是区间[1,+∞)上的减函数.若命题“p∨q”是真命题,求实数a的取值范围.
∵x∈[1,2]时,不等式x2+ax-2>0恒成立,
∴a> =
= -x在x∈[1,2]上恒成立,
-x在x∈[1,2]上恒成立,
令g(x)= -x,则g(x)在[1,2]上是减函数,
-x,则g(x)在[1,2]上是减函数,
∴g(x)max=g(1)=1,
∴a>1.即若命题p真,则a>1.
又∵函数f(x)=log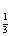 (x2-2ax+3a)是区间[1,+∞)上的减函数,
(x2-2ax+3a)是区间[1,+∞)上的减函数,
∴u(x)=x2-2ax+3a是[1,+∞)上的增函数,且u(x)=x2-2ax+3a>0在[1,+∞)上恒成立,
∴a≤1,u(1)>0,∴-1<a≤1,
即若命题q真,则-1<a≤1.
综上知,若命题“p∨q”是真命题,则a>-1.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 确定t的值,使S1与S2之和最小。
确定t的值,使S1与S2之和最小。
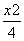 +
+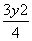 =1},B={y|y=x2},则A∩B=( )
=1},B={y|y=x2},则A∩B=( )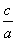 >
>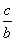 ”的逆否命题是真命题;
”的逆否命题是真命题;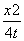 +
+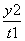 =1表示曲线C,给出以下命题:
=1表示曲线C,给出以下命题: .
. q:x2+y2>r2(x,y∈R,r>0),若p是q的充分不必要条件,则r的取值范围是________.
q:x2+y2>r2(x,y∈R,r>0),若p是q的充分不必要条件,则r的取值范围是________. 的定义域是________.
的定义域是________.