题目内容
9.已知函数$f(x)=xlnx-\frac{a}{2}{x^2}({a∈R})$.(1)当a=1时,求函数在点(1,-$\frac{1}{2}$)处的切线方程;
(2)若函数g(x)=f(x)-x有两个极值点x1,x2,求a的取值范围.
(3)在(2)的条件下,求证:$\frac{1}{ln{x}_{1}}$+$\frac{1}{ln{x}_{2}}$>2.
分析 (1)求出函数的导数,计算f′(1),求出切线方程即可;
(2)求出函数的导数,通过讨论a的范围,判断函数的单调性,从而确定a的范围即可;
(3)要证$\frac{1}{{ln{x_1}}}+\frac{1}{{ln{x_2}}}>2$,即证$ln\frac{x_2}{x_1}<\frac{x_2^2-x_1^2}{{2{x_1}{x_2}}}=\frac{1}{2}(\frac{x_2}{x_1}-\frac{x_1}{x_2})$,令$t=\frac{x_2}{x_1}>1$,即证$lnt<\frac{1}{2}(t-\frac{1}{t})$,设$φ(t)=lnt-\frac{1}{2}(t-\frac{1}{t})$,根据函数的单调性证明即可.
解答 解:(1)a=1时,f(x)=xlnx-$\frac{1}{2}$x2,
则f′(x)=lnx+1-x,
则f′(1)=0,
故切线方程是:y+$\frac{1}{2}$=0(x-1),
即y=-$\frac{1}{2}$;
(2)函数g(x)=f(x)-x有两个相异的极值点x1,x2,
即g′(x)=lnx-ax=0有两个不同的实数根,
①当a≤0时,g′(x)单调递增,
g′(x)=0不可能有两个不同的实根;
②当a>0时,设h(x)=lnx-ax,${h^'}(x)=\frac{1-ax}{x}$,
当$0<x<\frac{1}{a}$时,h′(x)>0,h(x)单调递增;
当$x>\frac{1}{a}$时,h′(x)<0,h(x)单调递减;
∴$h(\frac{1}{a})=-lna-1>0$,∴$0<a<\frac{1}{e}$,
(3)不妨设x2>x1>0,∵${g^'}({x_1})={g^'}({x_2})=0$,
∴lnx2-ax2=0,lnx1-ax1=0,lnx2-lnx1=a(x2-x1),
要证$\frac{1}{{ln{x_1}}}+\frac{1}{{ln{x_2}}}>2$,即证$\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}<\frac{{{x_2}+{x_1}}}{{2{x_1}{x_2}}}$,
即证$ln\frac{x_2}{x_1}<\frac{x_2^2-x_1^2}{{2{x_1}{x_2}}}=\frac{1}{2}(\frac{x_2}{x_1}-\frac{x_1}{x_2})$,
令$t=\frac{x_2}{x_1}>1$,即证$lnt<\frac{1}{2}(t-\frac{1}{t})$,设$φ(t)=lnt-\frac{1}{2}(t-\frac{1}{t})$,
则${φ^'}(t)=\frac{{2t-{t^2}-1}}{{2{t^2}}}=\frac{{-{{(t-1)}^2}}}{{2{t^2}}}<0$,
函数φ(t)在(1,+∞)单调递减,
∴φ(t)<φ(1)=0,
∴$\frac{1}{{ln{x_1}}}+\frac{1}{{ln{x_2}}}>2$.
点评 本题考查了求切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\sqrt{5}$ |
| A. | [-1,2) | B. | [-1,2] | C. | [2,+∞) | D. | [-1,+∞) |

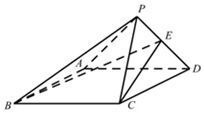 如图,四棱锥P-ABCD中,底面ABCD边长为4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;
如图,四棱锥P-ABCD中,底面ABCD边长为4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;