题目内容
19.已知x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$,若可行域内存在(x,y)使不等式2x+y+k≥0有解,则实数k的取值范围为[-4,+∞).分析 由约束条件作出可行域,可知当k≥0时,可行域内存在(x,y)使不等式2x+y+k≥0有解;当k<0时,要使可行域内存在(x,y)使不等式2x+y+k≥0有解,则目标函数z=2x+y+k的最大值2×2+0+k≥0,由此求得k的取值范围.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$作出可行域如图,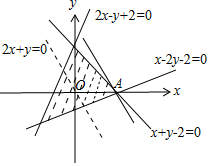
当k≥0时,可行域内存在(x,y)使不等式2x+y+k≥0有解;
当k<0时,要使可行域内存在(x,y)使不等式2x+y+k≥0有解,
则目标函数z=2x+y+k的最大值2×2+0+k≥0,即k≥-4.
综上,可行域内存在(x,y)使不等式2x+y+k≥0有解,实数k的取值范围为[-4,+∞).
故答案为:[-4,+∞).
点评 本题考查简单的线性规划,考查数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知三棱锥P-ABC的四个顶点均在同一个球面上,底面△ABC满足BA=BC=$\sqrt{6}$,$∠ABC=\frac{π}{2}$,若该三棱锥体积的最大值为3,则其外接球的体积为( )
| A. | 8π | B. | 16π | C. | $\frac{16}{3}$π | D. | $\frac{32}{3}$π |
10.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,|$\overrightarrow{a}$|=2,$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 12 |
4.已知△ABC中,内角A,B,C所对的边分别为a,b,c,若$\frac{b}{c}$=$\frac{cosA}{1+cosC}$,则sin(2A+$\frac{π}{6}$)的取值范围是( )
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,1] | D. | [-1,$\frac{1}{2}$) |
11.已知椭圆D:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴端点与焦点分别为双曲线E的焦点与实轴端点,若椭圆D与双曲线E的一个交点在直线y=2x上,则椭圆D的离心率为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{3-2\sqrt{2}}{2}$ |