题目内容
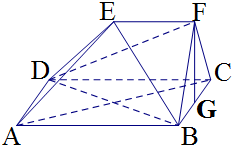
 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,CF⊥FB,BF=CF,G为BC的中点,
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,CF⊥FB,BF=CF,G为BC的中点,(Ⅰ)求证:FG∥平面BDE;
(Ⅱ)求平面BDE与平面BCF所成锐二面角的大小;
(Ⅲ)求四面体B-DEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)运用中的确定EO∥FG,再运用定理判断,
(Ⅱ)判断:平面BDE⊥平面ABCD,平面ABCD⊥平面BFC,得出∠BDC为平面BDE与平面BCF所成锐二面角的平面角,很容易就求解了.
(Ⅲ)求出底面积,高,运用体积公式求解即可.
(Ⅱ)判断:平面BDE⊥平面ABCD,平面ABCD⊥平面BFC,得出∠BDC为平面BDE与平面BCF所成锐二面角的平面角,很容易就求解了.
(Ⅲ)求出底面积,高,运用体积公式求解即可.
解答:
(Ⅰ)证明:设AC与BD交于点O,则O为AC的中点,
连结EC,CG,由于G为BC的中点,
故GO
AB,又EF
AB,
∴GO
EF,∴四边形EOGF是平行四边形,
∴EO∥FG,
∵EO?平面EDB,FG不包含于平面EDB,
∴FG∥平面BDE.
(Ⅱ)在Rt△BCF中,BF=CF,G为BC的中点,
∵EF⊥FB,CF⊥FB,
∴BF⊥平面CDEF,
∴CD⊥BF,
∵CD⊥BC,
∴CD⊥平面BFC,
∴平面ABCD⊥平面BFC,
∵FG⊥BC,EO∥GF
∴FG⊥平面ABCD,EO⊥平面ABCD,
∴平面BDE⊥平面ABCD,
∴∠BDC为平面BDE与平面BCF所成锐二面角的平面角,
∵四边形ABCD是正方形,∴二面角的大小45°;
(Ⅲ)△DEF的面积为
×EF×FC=
×1×
=
三棱锥B-DEF的高为BF=
,
∴三棱锥B-DEF的体积为
×
×
=
故四面体B-DEF的体积为:
连结EC,CG,由于G为BC的中点,
故GO
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴GO
| ∥ |
. |
∴EO∥FG,
∵EO?平面EDB,FG不包含于平面EDB,
∴FG∥平面BDE.
(Ⅱ)在Rt△BCF中,BF=CF,G为BC的中点,
∵EF⊥FB,CF⊥FB,
∴BF⊥平面CDEF,
∴CD⊥BF,
∵CD⊥BC,
∴CD⊥平面BFC,
∴平面ABCD⊥平面BFC,
∵FG⊥BC,EO∥GF
∴FG⊥平面ABCD,EO⊥平面ABCD,
∴平面BDE⊥平面ABCD,
∴∠BDC为平面BDE与平面BCF所成锐二面角的平面角,
∵四边形ABCD是正方形,∴二面角的大小45°;
(Ⅲ)△DEF的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
三棱锥B-DEF的高为BF=
| 2 |
∴三棱锥B-DEF的体积为
| 1 |
| 3 |
| ||
| 2 |
| 2 |
| 1 |
| 3 |
故四面体B-DEF的体积为:
| 1 |
| 3 |

点评:本题综合考察了空间几何体中直线,平面的平行,垂直问题,求解有关的几何体的体积,夹角问题.属于难题.

练习册系列答案
相关题目
设全集U=R,A={x|x>0},B={x|x>1},则A∩∁UB=( )
| A、{x|0≤x<1} |
| B、{x|0<x≤1} |
| C、{x|x<0} |
| D、{|x>1} |
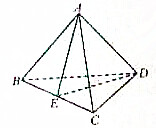 在所有棱长均为2的四面体ABCD中,E是BC的中点,写出四面体中与平面AED垂直的面,并说明理由.
在所有棱长均为2的四面体ABCD中,E是BC的中点,写出四面体中与平面AED垂直的面,并说明理由.