题目内容
17.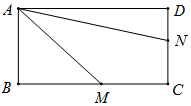 如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )
如图,某地区有四个公司分别位于矩形ABCD的四个顶点,且AB=1km,BC=2km,四个公司商量准备在矩形空地中规划一个三角形区域AMN种植花草,其中M,N分别在直线BC,CD上运动,∠MAN=30°,设∠BAM=α,当三角AMN的面积最小时,此时α=( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{12}$ |
分析 由已知可求AM=$\frac{1}{cosα}$,AN=$\frac{2}{cos(\frac{π}{3}-α)}$,可求三角形面积,利用三角函数的恒等变换化简得到S△AMN关于α的三角函数,利用正弦函数的性质结合α的范围即可计算得解.
解答 解:由于:∠BAM=α,
由题意可知,AM=$\frac{1}{cosα}$,AN=$\frac{2}{cos(\frac{π}{3}-α)}$,
则S△AMN=$\frac{1}{2}$AM•ANsin$\frac{π}{6}$=$\frac{1}{2}×$$\frac{1}{cosα}$×$\frac{2}{cos(\frac{π}{3}-α)}$=$\frac{1}{\frac{1}{2}co{s}^{2}α+\frac{\sqrt{3}}{2}sinαcosα}$=$\frac{1}{\frac{1}{2}(\frac{1}{2}cos2α+\frac{\sqrt{3}}{2}sin2α)+\frac{1}{4}}$
=$\frac{4}{2sin(2α+\frac{π}{6})+1}$,
当$α=\frac{π}{6}$时,三角形AMN面积最小.
故选:B.
点评 本题考查了三角函数的恒等变换,三角形的面积公式,考查了转化思想和数形结合思想的应用,属于中档题.

练习册系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}x,x>0}\\{{3}^{x},x≤0}\end{array}\right.$,则f(f(9))的值为( )
| A. | -$\frac{1}{9}$ | B. | -9 | C. | $\frac{1}{9}$ | D. | 9 |
8.一个圆柱的正视图是面积为6的矩形,它的侧面积为( )
| A. | 8π | B. | 6π | C. | 4π | D. | 3π |
5.设复数$z=\frac{{2{i^3}}}{i-1}$(i为虚数单位),z则的虚部为( )
| A. | i | B. | -i | C. | -1 | D. | 1 |
12.设双曲线以椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1长轴的两个端点为焦点,以椭圆的焦点为顶点,则双曲线的渐近线的斜率为( )
| A. | ±$\frac{5}{4}$ | B. | ±$\frac{4}{3}$ | C. | ±$\frac{4}{5}$ | D. | ±$\frac{3}{4}$ |
2.如图是某几何体的三视图,则该几何体的体积为( )


| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
9.“n>m>0”是方程“mx2+ny2=1表示焦点在x轴上的椭圆”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知抛物线x2=2py(p>0)的准线经过点(0,-2),则抛物线的焦点坐标为( )
| A. | (0,1) | B. | (0,2) | C. | (1,0) | D. | (2,0) (第4题图) |