题目内容
7.在直三棱柱ABC-A1B1C1中,AA1=AB=BC=2,$∠ABC=\frac{π}{2}$,E,F分别为棱AB,AC的中点,则直线A1E和C1F的夹角余弦值为( )| A. | $\frac{{\sqrt{30}}}{10}$ | B. | $\frac{{\sqrt{30}}}{6}$ | C. | $\frac{{\sqrt{10}}}{6}$ | D. | $\frac{{2\sqrt{30}}}{15}$ |
分析 如图所示,建立空间直角坐标系.利用向量夹角公式即可得出.
解答 解:如图所示,建立空间直角坐标系.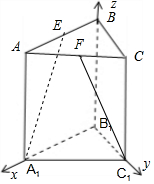
A1(2,0,0),E(1,0,2),C1(0,2,0),F(1,1,2),
则$\overrightarrow{{A}_{1}E}$=(-1,0,2),$\overrightarrow{{C}_{1}F}$=(1,-1,2),
∴$\overrightarrow{{A}_{1}E}$•$\overrightarrow{{C}_{1}F}$=-1+0+4=3,
$cos<\overrightarrow{{A}_{1}E},\overrightarrow{{C}_{1}F}>$=$\frac{\overrightarrow{{A}_{1}E}•\overrightarrow{{C}_{1}F}}{|\overrightarrow{{A}_{1}E}||\overrightarrow{{C}_{1}F}|}$=$\frac{3}{\sqrt{5}×\sqrt{6}}$=$\frac{\sqrt{30}}{10}$.
∴直线A1E和C1F的夹角余弦值为$\frac{\sqrt{30}}{10}$.
故选:A.
点评 本题考查了数量积运算性质、向量夹角公式、异面直线所成的角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.下列函数中,最小正周期为π且在(0,$\frac{π}{2}$)是减函数的是( )
| A. | y=cos(2x+$\frac{π}{2}$) | B. | y=|sin(x+$\frac{π}{3}$)| | C. | y=2cos2x-3 | D. | y=-tan2x |
2.如图是某几何体的三视图,则该几何体的体积为( )


| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
12.已知f(x)是定义在R上的偶函数,其导函数为f′(x),若f′(x)<f(x),且f(x+1)=f(3-x),f (2011)=3,则不等式f (x)<3ex-1的解集为( )
| A. | (e,+∞) | B. | (1,+∞) | C. | (-∞,0) | D. | (-∞,$\frac{1}{e}$) |
19.袋中有大小,形状相同的红球,黑球各一个,现有放回地随机摸取3次,每次摸出一个球.若摸到红球得2分,摸到黑球得1分,则3次摸球所得总分为5分的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
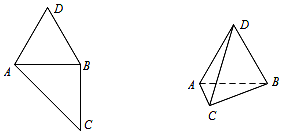 如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.
如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.