Question

函数f（x）=2sin（ωx+φ）(ω＞0，0＜φ＜

π

2

)的部分图象如图所示，该图象与y轴交于点F（0，1），与x轴交于点B，C，M为最高点，且△MBC的面积为π．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）已知f（α）=

8

5

，α∈(

π

2

，π)，求sin(α+

5

12

π)的值．

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

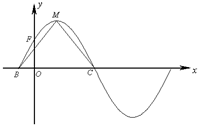
分析：（Ⅰ）由△MBC的面积为π可得BC长，进而求出周期，确定ω的值，再由函数f（x）的图象与y轴交于点F（0，1）及0＜ϕ＜

π

2

，可得φ的值，进而可得函数f（x）的解析式；
（Ⅱ）已知f（α）=

8

5

，α∈(

π

2

，π)，可得sin（α+

π

6

）=

4

5

，cos（α+

π

6

）=-

3

5

，进而由sin(α+

5

12

π)=sin[（α+

π

6

）+

π

4

]，结合两角和的正弦公式，可得答案．

解答： 解：（I）∵函数f（x）=2sin（ωx+φ）的最大值为2，
故△MBC的面积S=

1

2

×2×BC=π，
∴函数f（x）的周期T=2π．
即ω=1；
由函数f（x）的图象与y轴交于点F（0，1），
故f（0）=2sinφ=1，得sinφ=

1

2

，
∵0＜ϕ＜

π

2

，
∴φ=

π

6

，
∴f（x）=2sin（x+

π

6

）．
（Ⅱ）∵f（α）=2sin（α+

π

6

）=

8

5

，α∈(

π

2

，π)，
∴sin（α+

π

6

）=

4

5

，cos（α+

π

6

）=-

3

5

，
∴sin(α+

5

12

π)=sin[（α+

π

6

）+

π

4

]=

2

2

×（

4

5

-

3

5

）=

2

10

．

点评：本题考查的知识点是正弦型函数的图象和性质，其中根据已知确定ω和φ的值，求出函数解析式，是解答的关键．