题目内容
定义在R上的函数f（x）满足：f（x+2）=
，当x∈（0，4）时，f（x）=x2-1，则f（2007）= ．
| 1 |
| f(x) |
考点：函数的值
专题：
分析：由已知得f(x+4)=
=f(x)，从而f（2007）=f（3）=32-1=8．
| 1 |
| f(x+2) |
解答：
解：∵定义在R上的函数f（x）满足：f（x+2）=
，
∴f(x+4)=
=f(x)，
∵当x∈（0，4）时，f（x）=x2-1，
∴f（2007）=f（3）=32-1=8．
故答案为：8．
| 1 |
| f(x) |
∴f(x+4)=
| 1 |
| f(x+2) |
∵当x∈（0，4）时，f（x）=x2-1，
∴f（2007）=f（3）=32-1=8．
故答案为：8．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函性质的合理运用．
练习册系列答案
相关题目
设集合S={x|2x＞
}，T={x|-4≤x≤1}，则S∩T=（ ）
| 1 |
| 4 |
| A、[-4，+∞） |
| B、（-2，+∞） |
| C、[-4，1] |
| D、（-2，1] |
已知函数f（x）=2sin（
x+
），则f（1）+f（2）+…+f（2012）+f（2013）的值是（ ）
| π |
| 3 |
| 2π |
| 3 |
A、-2
| ||
B、-
| ||
C、
| ||
| D、0 |
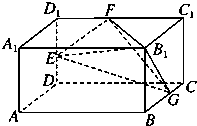如图，长方体AC1中，AB=2，BC=AA1=1．E、F、G分别为棱DD1、D1C1、BC的中点．
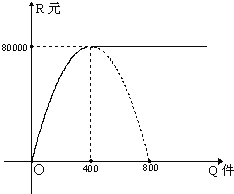某工厂生产某种产品，固定成本为20000元，每生产一件产品，成本增加100元．已知总收益R是年产量Q（件）的函数，其图象（图中实线部分）如下：当年产量Q在[0，400]内时，为抛物线的一段；当年产量Q＞400件时，为一条射线．