题目内容
是否存在实数β使复数cosβ+isinβ对应点在直线2x+2y-3=0上?若存在,求出β;若不存在,说明理由.
考点:复数的代数表示法及其几何意义
专题:三角函数的求值,数系的扩充和复数
分析:根据复数的几何意义以及点和直线的位置关系进行判断即可.
解答:
解:复数对应的点的坐标为(cosβ,sinβ),
若点在直线上,则2cosβ+2sinβ-3=0,
即cosβ+sinβ=
,
∵cosβ+sinβ=
sin(β+
)∈[-
,
],
而
>
,
∴方程cosβ+sinβ=
无解,
即不存在实数β使复数cosβ+isinβ对应点在直线2x+2y-3=0上.
若点在直线上,则2cosβ+2sinβ-3=0,
即cosβ+sinβ=
| 3 |
| 2 |
∵cosβ+sinβ=
| 2 |
| π |
| 4 |
| 2 |
| 2 |
而
| 3 |
| 2 |
| 2 |
∴方程cosβ+sinβ=
| 3 |
| 2 |
即不存在实数β使复数cosβ+isinβ对应点在直线2x+2y-3=0上.
点评:本题主要考查复数的几何意义,以及三角函数的性质,利用辅助角公式将三角方程化简是解决本题的关键.

练习册系列答案
相关题目
直线y=ax+b(a+b=0)的图象可能是( )
A、 |
B、 |
C、 |
D、 |
已知等比数列{an}中,a1+a6=33,a2a5=32,公比q>1,则a3+a8=( )
| A、66 | B、132 |
| C、64 | D、128 |
下面不等式成立的是( )
| A、1.72.5>1.73 |
| B、log0.23<log0.25 |
| C、1.73.1<0.93.1 |
| D、log30.2<log0.20.3 |
图中阴影部分表示的集合是( )


| A、∁U(A∩B) |
| B、∁U(A∪B) |
| C、A∩(∁UB) |
| D、(∁UA)∩B |
已知集合A={x|1<x<5},B={x|x2-3x+2<0},则CAB=( )
| A、{x|2<x<5} |
| B、{x|2≤x<5} |
| C、{x|2≤x≤5} |
| D、∅ |
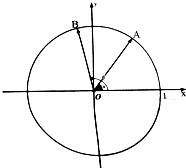 如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,
如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,