题目内容
7.不等式|x+3|+|x-1|<a2-3a有解的实数a的取值范围是( )| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
分析 由已知中的不等式|x+3|+|x-1|<a2-3a,我们可以构造绝对值函数,根据绝对值的几何意义,我们易求出对应函数y=|x+3|+|x-1|的值域,进而得到实数a的取值范围.
解答 解:令y=|x+3|+|x-1|
则函数y=|x+3|+|x-1|≥|x+3-x+1|=4,
∴函数的值域为[4,+∞)
若不等式|x+3|+|x-1|<a2-3a有解,
则a2-3a>4,解得:a>4或a<-1,
故实数a的取值范围是(-∞,-1)∪(4,+∞),
故选:A.
点评 本题考查的知识点是绝对值三角不等式,其中构造绝对值函数,并根据绝对值的几何意义,判断出函数y=|x+3|+|x-1|的值域是解答本题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
17.“点P的轨迹方程为y=|x|”是“点P到两条坐标轴距离相等”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
12.已知向量$\vec a$,$\vec b$的夹角为120°,且$|\vec a|=2$,$|\vec b|=1$,$|{\vec a+2\vec b}|$=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | 7 | D. | 2 |
16.已知 a,b是两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )
| A. | 若a∥α,b∥α,则a∥b | B. | 若α⊥β,a?α,b?β,则a⊥b | ||
| C. | 若a⊥b,b⊥α,则a∥α | D. | 若α∥β,a?α,则a∥β |
17.设某几何体的三视图如图(长度单位为cm),则该几何体的最长的棱为( )cm
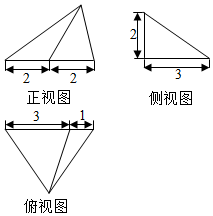

| A. | 4cm | B. | $\sqrt{13}$cm | C. | $\sqrt{14}$cm | D. | $\sqrt{15}$cm |