题目内容
17．设某几何体的三视图如图（长度单位为cm），则该几何体的最长的棱为（ ）cm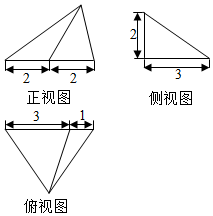
| A． | 4cm | B． | $\sqrt{13}$cm | C． | $\sqrt{14}$cm | D． | $\sqrt{15}$cm |
分析 根据几何体的三视图，得出该几何体是侧面垂直于底面的三棱锥，结合图形，求出各条棱长，即可得出最长的侧棱长是多少
解答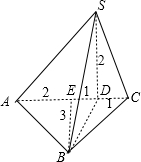 
解：根据几何体的三视图，得
该几何体是如图所示的三棱锥S-ABC，且侧面SAC⊥底面ABC；
又SD⊥AC于D，
∴SD⊥底面ABC；
又BE⊥AC与E，
∴AB=BC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$cm；
SC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$cm，
SA=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$cm；
AC=4cm，
BD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$cm，
∴SB=$\sqrt{{2}^{2}+{\sqrt{10}}^{2}}$=$\sqrt{14}$cm；
∴最长的棱长是AC，长4cm，
故选：A
点评 本题考查了空间几何体三视图的应用问题，解题的关键是由三视图还原出几何体的结构特征，是中档题目．
练习册系列答案
相关题目
7．不等式|x+3|+|x-1|＜a2-3a有解的实数a的取值范围是（ ）
| A． | （-∞，-1）∪（4，+∞） | B． | （-1，4） | C． | （-∞，-4）∪（1，+∞） | D． | （-4，1） |
8．从3个英语教师和5个语文教师中选取4名教师参加外事活动，其中至少要有一名英语教师，则不同的选法共有（ ）
| A． | $A_3^1A_5^3+A_3^2A_5^2+A_3^3A_5^1$ | |
| B． | $C_3^1C_5^3+C_3^2C_5^2+C_3^3C_5^1$ | |
| C． | $C_3^1C_7^3$ | |
| D． | $（{C_3^1C_5^3+C_3^2C_5^2+C_3^3C_5^1}）A_4^4$ |
9．在△ABC中，角A，B，C的对边分别是a，b，c，面积为S，若S≥$\frac{1}{2}$ab，b2+ac=a2+c2，则a：b：c等于（ ）
| A． | 3：4：5 | B． | 1：1：$\sqrt{2}$ | C． | 1：$\sqrt{2}$：$\sqrt{3}$ | D． | 1：$\sqrt{3}$：2 |