题目内容
17.“点P的轨迹方程为y=|x|”是“点P到两条坐标轴距离相等”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
分析 根据充分条件和必要条件的定义进行判断即可.
解答 解:设动点P(x,y),则它到两坐标轴x,y距离的分别为|y|,|x|,
∴到两坐标轴距离相等的点的轨迹方程是|x|=|y|,即y=±|x|,
“点P的轨迹方程为y=|x|”是“点P到两条坐标轴距离相等”的充分不必要条件,
故选:A.
点评 本题主要考查充分条件和必要条件的判断,根据点到坐标轴距离相等的条件求出对应的关系是解决本题的关键.比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知命题p:?x∈R,log2x=2015,则¬p为( )
| A. | ?x∉R,log2x=2015 | B. | ?x∈R,log2x≠2015 | ||
| C. | ?x0∈R,log2x0=2015 | D. | ?x0∈R,log2x0≠2015 |
6.为了得到函数y=$\sqrt{2}$sin3x的图象,可以将函数y=$\sqrt{2}$sin(3x+$\frac{π}{2}$)的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
7.不等式|x+3|+|x-1|<a2-3a有解的实数a的取值范围是( )
| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
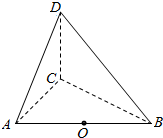 如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.
如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.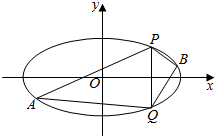 已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.
已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.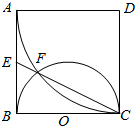 如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.