题目内容
已知f(x)=sin2x+|sin2x|(x∈R),则下列判断正确的是( )
| A、f(x)是周期为2π的奇函数 |
| B、f(x)是值域为[0,2]周期为π的函数 |
| C、f(x)是周期为2π的偶函数 |
| D、f(x)是值域为[0,1]周期为π的函数 |
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:利用绝对值的代数意义化简函数f(x),并画出此分段函数的图象,根据函数的图象即可得到函数的最小正周期和值域.
解答:
解:若2kπ≤2x≤2kπ+π,即kπ≤x≤kπ+
时,sin2x≥0,
f(x)=sin2x+|sin2x|=2sin2x;
若2kπ+π≤2x≤2kπ+2π,即kπ+
≤x≤kπ+π时,sin2x<0,
f(x)=sin2x+|sin2x|=0,
作出函数图象,如下图:
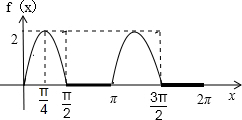
根据图象可知f(x)为周期函数,最小正周期为π,
函数的值域为[0,2].
故选:B
| π |
| 2 |
f(x)=sin2x+|sin2x|=2sin2x;
若2kπ+π≤2x≤2kπ+2π,即kπ+
| π |
| 2 |
f(x)=sin2x+|sin2x|=0,
作出函数图象,如下图:

根据图象可知f(x)为周期函数,最小正周期为π,
函数的值域为[0,2].
故选:B
点评:本题主要考查函数的周期性及其求法,涉及的知识有绝对值的代数意义,以及正弦函数的图象与性质,利用了分类讨论及数形结合的数学思想,根据题意正确画出已知函数的图象是解本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
指数函数y=3x,当x<0时,y的取值范围是( )
| A、y>1 | B、y<1 |
| C、0<y<1 | D、y<0 |
过点A(0,2 ),B (2,0)的直线的斜率是( )
| A、2 | B、1 | C、-2 | D、-1 |
命题“若α=
,则tanα=1”的否命题是( )
| π |
| 4 |
A、若α≠
| ||
B、若α=
| ||
C、若tanα≠1,则α≠
| ||
D、若tanα≠1,则α=
|