题目内容
18.已知W=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,在复平面内,将1、W、W2所对应的三点连接起来组成什么图形?其面积是多少?分析 设1、W、W2所对应的三点分别为A,B,C,分别求出其坐标为A(1,0),B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),C(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),得到图形为等腰三角形,求出其面积即可.
解答  解:∵W=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,
解:∵W=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,
∴W2=-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i,
设1、W、W2所对应的三点分别为A,B,C,
其坐标分别为A(1,0),B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),C(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
∴|AB|=|AC|
∴将1、W、W2所对应的三点连接起来组成等腰三角形,
∴S△ABC=$\frac{1}{2}$×(1+$\frac{1}{2}$)×($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$)=$\frac{3\sqrt{3}}{4}$.
点评 本题考查了复数的计算以及复数的几何意义,属于基础题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

 B.
B.  C.
C.  D.
D.
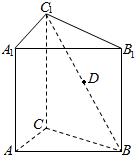 如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.