题目内容
11．
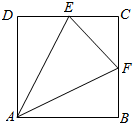如图，正方形ABCD中，E、F分别为CD、BC的中点，沿AE、AF、EF将其折成一个多面体，则此多面体是直三棱锥．
分析 根据折叠前、后的图形情况，结合线面垂直的判定定理，得出该多面体是直三棱锥．
解答 解：在正方形ABCD中，AB⊥BF，AD⊥DE，折叠后的图形B，C，D三点重合，
∴三棱锥A-CEF中，AC⊥CE，AC⊥CF，CE∩CF=C，
∴AC⊥平面CEF，三棱锥A-CEF是直三棱锥．
故答案为：直三棱锥．
点评 本题考查了平面图形的折叠问题，解题时应明确折叠前后的图形变化情况，是基础题目．
练习册系列答案
快乐5加2金卷系列答案
相关题目
5．设单位向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|3$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$，则|3$\overrightarrow{a}$-$\overrightarrow{b}$|=（ ）
| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
16．设a、b为两条不同的直线，α为一个平面，下列命题中为真命题的是（ ）
| A． | 若a∥b，a∥α，则b∥α | B． | 若a⊥b，a∥α，则b⊥α | C． | 若a∥b，a⊥α，则b⊥α | D． | 若a⊥b，a⊥α，则b∥α |
20．
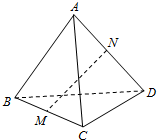如图，在四面体ABCD，AB=CD，M，N分别是BC，AD的中点，若AB与CD所成的角的大小为60°，则MN和CD所成的角的大小为（ ）
如图，在四面体ABCD，AB=CD，M，N分别是BC，AD的中点，若AB与CD所成的角的大小为60°，则MN和CD所成的角的大小为（ ）| A． | 30° | B． | 60° | C． | 30°或60° | D． | 15°或60° |
1．
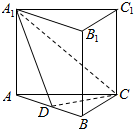如图，三棱柱ABC-A1B1C1的棱长都相等，侧棱垂直于底面，点D是棱AB的中点，则直线AC与平面A1DC所成角的正弦值为（ ）
如图，三棱柱ABC-A1B1C1的棱长都相等，侧棱垂直于底面，点D是棱AB的中点，则直线AC与平面A1DC所成角的正弦值为（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{\sqrt{6}}{4}$ |