题目内容
已知函数f（x）的图象是连续不断的，有如下的x，f（x）对应值表：
则函数f（x）至少有 个零点．
| X | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 |
| F（x） | -3.51 | 1.02 | 2.37 | 1.56 | -0.38 | 1.23 | 2.77 | 3.45 | 4.89 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：利用函数零点判断定理求解．
解答：
解：∵函数f（x）的图象是连续不断的，
且由f（x）对应值表知：
f（-2）f（-1.5）＜0，
f（-0.5）f（0）＜0，
f（0）f（0.5）＜0，
∴由函数零点判断定理知函数f（x）至少有 3个零点．
故答案为：3．
且由f（x）对应值表知：
f（-2）f（-1.5）＜0，
f（-0.5）f（0）＜0，
f（0）f（0.5）＜0，
∴由函数零点判断定理知函数f（x）至少有 3个零点．
故答案为：3．
点评：本题考查函数零点个数的求法，是基础题，解题时要认真审题，注意函数零点判断定理的灵活运用．
练习册系列答案
相关题目
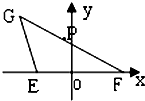已知E、F是x轴上的点，坐标原点O为线段EF的中点，G、P是坐标平面上的动点，点P在线段FG上，|