题目内容
 如图,在四棱锥V-ABC中,VA=VC=AB=BC=1,∠AVC=∠ABC=90°,二面角V-AC-B的大小为60°.
如图,在四棱锥V-ABC中,VA=VC=AB=BC=1,∠AVC=∠ABC=90°,二面角V-AC-B的大小为60°.(1)求证:VB⊥AC;
(2)求四棱锥V-ABC的体积.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)取AC的中点为D,连接VD,BD,通过证明直线AC⊥平面VDB,然后证明VB⊥AC;
(2)证明△VDB为等边三角形,利用VV-ABC=
S△VDB•AC求三棱锥V-ABC的体积.
(2)证明△VDB为等边三角形,利用VV-ABC=
| 1 |
| 3 |
解答:
 (1)证明:取AC的中点为D,连接VD,BD.
(1)证明:取AC的中点为D,连接VD,BD.
∵VA=VB,∴AC⊥VD;同理AC⊥BD.
于是AC⊥平面VDB.
又VB?平面VDB,故VB⊥AC.
(2)解:由(1)知AC⊥平面VDB,
∴∠VDB是二面角V-AC-B的平面角,
∴∠VDB=60°,
∵∠AVC=∠ABC=90°,VA=VC=AB=BC=1,
∴VD=DB=
,
∴△VDB为等边三角形,
∴VV-ABC=
S△VDB•AC=
•
•(
)2•
=
.
 (1)证明:取AC的中点为D,连接VD,BD.
(1)证明:取AC的中点为D,连接VD,BD.∵VA=VB,∴AC⊥VD;同理AC⊥BD.
于是AC⊥平面VDB.
又VB?平面VDB,故VB⊥AC.
(2)解:由(1)知AC⊥平面VDB,
∴∠VDB是二面角V-AC-B的平面角,
∴∠VDB=60°,
∵∠AVC=∠ABC=90°,VA=VC=AB=BC=1,
∴VD=DB=
| ||
| 2 |
∴△VDB为等边三角形,
∴VV-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 2 |
| 2 |
| ||
| 24 |
点评:本题考查直线与平面的垂直的性质定理以及棱锥体积的求法,考查逻辑思维能力与计算能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
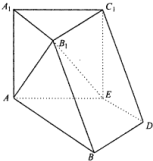 如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.