题目内容
18．若f（x）在R上可导，f（x）=x2+2f′（2）x+3，则f'（0）=-8．分析 首先对已知等式求导，然后对x赋值为2，0，得到所求．
解答 解：由已知得到f'（x）=[x2+2f′（2）x+3]'=2x+2f'（2），
取x=2，得到f'（2）=4+2f'（2），得到f'（2）=-4，
所以f'（0）=2f'（2）=-8；
故答案为：-8．
点评 本题考查了函数的求导以及赋值求函数值；属于基础题．
练习册系列答案
相关题目
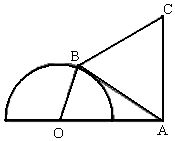如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC．当四边形OACB面积最大时，∠AOB=150°．
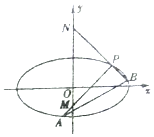已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，以椭圆的四个顶点为顶点的四边形的面积为8．
如图，在各棱长为2的三棱柱ABC-A1B1C1中，侧面A1ACC1⊥底面ABC，∠A1AC=60°．
10．下列命题中：
①若x2-3x+2=0，则x=1或x=2
②若-2≤x≤3，则（x+2）（x-3）≤0
③若x=y=0，则x2+y2=0
④若x、y∈N*，x+y是奇数，则x、y中一个是奇数，一个是偶数．
那么（ ）
①若x2-3x+2=0，则x=1或x=2
②若-2≤x≤3，则（x+2）（x-3）≤0
③若x=y=0，则x2+y2=0
④若x、y∈N*，x+y是奇数，则x、y中一个是奇数，一个是偶数．
那么（ ）
| A． | ①的逆命题为真 | B． | ②的否命题为假 | C． | ③的逆否命题为假 | D． | ④的逆命题为假 |