题目内容
7.定义在(0,+∞)上的函数f(x)满足x2f′(x)+1>0,f(1)=5,则不等式$f(x)<\frac{1}{x}+4$的解集为(0,1).分析 设$g(x)=f(x)-\frac{1}{x}-4$对其求导,结合已知不等式得到其单调性,所求不等式转利用单调性得到自变量的大小,即x范围.
解答 解:由x2f′(x)+1>0,设$g(x)=f(x)-\frac{1}{x}-4$,则$g′(x)=f′(x)+\frac{1}{x^2}$=$\frac{{x}^{2}f'(x)+1}{{x}^{2}}$>0.
故函数g(x)在(0,+∞)上单调递增,又g(1)=0,故g(x)<0的解集为(0,1),
即$f(x)<\frac{1}{x}-4$的解集为(0,1).
故答案为:(0,1).
点评 本题考查了抽象不等式的解法;关键是正确构造新函数,利用已知不等式得到函数的单调性.

练习册系列答案
相关题目
17.已知数列{an}是等差数列,a1+a3=2,a3+a5=4,则a5+a7=( )
| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
19.已知△ABC中,BC=$\sqrt{3}$,AC=2,角A=60°,则边AB=( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
17.执行如图所示的程序框图,如果输入n=5,则输出的S值为( )
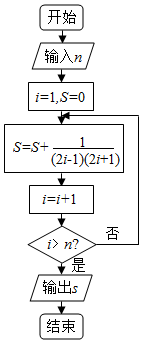

| A. | $\frac{4}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{5}{11}$ | D. | $\frac{10}{11}$ |