题目内容
8.已知a,b是不相等的正实数,则$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$与$\sqrt{a}$+$\sqrt{b}$两个数的大小顺序是$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$.分析 作差,分解,利用实数的性质,可得:($\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$)-($\sqrt{a}$+$\sqrt{b}$)=$\frac{(\sqrt{a}-\sqrt{b})^{2}(\sqrt{a}+\sqrt{b})}{\sqrt{ab}}$>0.进而得到结论.
解答 解:($\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$)-($\sqrt{a}$+$\sqrt{b}$)
=$\frac{a-b}{\sqrt{b}}$-$\frac{a-b}{\sqrt{a}}$
=(a-b)$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{ab}}$
=$\frac{(\sqrt{a}-\sqrt{b})^{2}(\sqrt{a}+\sqrt{b})}{\sqrt{ab}}$>0.
故$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$,
故答案为:$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$
点评 本题考查的知识点是作差法比较数的大小,不等式的证明,难度中档.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
19.已知△ABC中,BC=$\sqrt{3}$,AC=2,角A=60°,则边AB=( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
3.将一个质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b,若已知出现了点数5,则使不等式a-b+3>0成立的事件发生的概率为( )
| A. | $\frac{33}{36}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{11}$ | D. | $\frac{5}{18}$ |
17.执行如图所示的程序框图,如果输入n=5,则输出的S值为( )
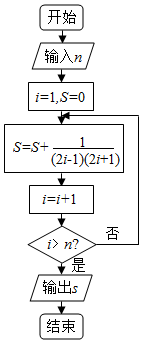

| A. | $\frac{4}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{5}{11}$ | D. | $\frac{10}{11}$ |
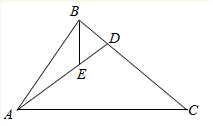 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.