题目内容
18．将数字“123367”重新排列后得到不同的偶数个数为（ ）| A． | 72 | B． | 120 | C． | 192 | D． | 240 |
分析 根据题意，分2步进行分析：①．在2、6中任选1个安排在个位数字，②由倍分法分析前5个数位的排法数目，由分步计数原理计算可得答案．
解答 解：根据题意，分2步进行分析：
①、要求为偶数，则其个位数字为2或6，有2种情况，
②、将其余5个数字全排列，安排在前5个数位，由于其中有2个“3”，
则前5个数位有$\frac{{A}_{5}^{5}}{2}$=60种情况，
则可以得到2×60=120个不同的偶数；
故选：B
点评 本题考查排列、组合的应用，注意数字中有两个“3”．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．首项为-12的等差数列，从第10项起开始为正数，则公差d的取值范围是（ ）
| A． | d＞$\frac{8}{3}$ | B． | d＜3 | C． | $\frac{8}{3}$≤d＜3 | D． | $\frac{4}{3}$＜d≤$\frac{3}{2}$ |
如图，在四棱锥P-ABCD中，底面是直角梯形ABCD，其中AD⊥AB，CD∥AB，AB=4，CD=2，侧面PAD是边长为2的等边三角形，且与底面ABCD垂直，E为PA的中点．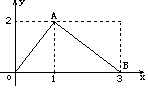
函数f（x）的图象是如图所示的折线段OAB，点A坐标为（1，2），点B坐标为（3，0），
10．在等差数列{an}中，a3=0，a7-2a4=-1，则公差d等于（ ）
| A． | -2 | B． | $\frac{1}{2}$ | C． | 2 | D． | -$\frac{1}{2}$ |
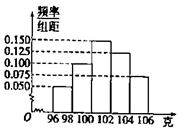某工厂对一批产品进行了抽样检测，如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），（104，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（ ）