题目内容
下列关系式中,正确的是( )
| A、{2,3}≠{3,2} |
| B、{(a,b)}={(b,a)} |
| C、{x|y=x2+1}={y|y=x+1} |
| D、{y|y=x2+1}={x|y=x+1} |
考点:集合的相等
专题:集合
分析:根据集合的概念和表示方法逐项判断即可.
解答:
解:A、集合的元素具有无序性,所以{2,3}={3,2},故A错误;
B、两个集合都是点集,而点使用有序数对表示(a,b)与(b,a)不一定表示同一个点,除非a=b,所以两个集合不一定相等,故B错误;
C、使用描述法表示集合时,要注意集合的代表字母,{x|y=x2+1}表示y=x2+1的定义域R,{y|y=x+1}表示函数y=x+1的值域R,所以两集合相等,故C正确;
D、同C,{y|y=x2+1}={y|y≥1},{x|y=x+1}=R,所以集合不相等,故D错误;
故选:C.
B、两个集合都是点集,而点使用有序数对表示(a,b)与(b,a)不一定表示同一个点,除非a=b,所以两个集合不一定相等,故B错误;
C、使用描述法表示集合时,要注意集合的代表字母,{x|y=x2+1}表示y=x2+1的定义域R,{y|y=x+1}表示函数y=x+1的值域R,所以两集合相等,故C正确;
D、同C,{y|y=x2+1}={y|y≥1},{x|y=x+1}=R,所以集合不相等,故D错误;
故选:C.
点评:本题考查集合的表示方法和集合相等,注意描述法中的集合的代表字母.

练习册系列答案
相关题目
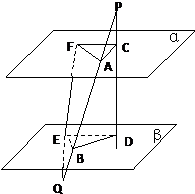 如图,线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,△ACF的面积为72,求△BDE的面积.
如图,线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,△ACF的面积为72,求△BDE的面积.