题目内容
18.某企业有员工75人,其中男员工有30人,为作某项调查,拟采用分层抽样的方法抽取容量为20的样本,则女员工应抽取的人数是12.分析 分层抽样应按各层所占的比例从总体中抽取,即可得出结论.
解答 解:总体的个数是75人,要抽一个20人的样本,则每个个体被抽到的概率是$\frac{20}{75}$=$\frac{4}{15}$,
女员工应选取的人数(75-30)×$\frac{4}{15}$=12人,
故答案为:12.
点评 本题考查分层抽样方法,本题解题的关键是注意在抽样过程中每个个体被抽到的概率相等,这是解题的依据.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10.设z1,z2是复数,则下列结论中正确的是( )
| A. | 若${z_1}^2+{z_2}^2>0$,则 ${z_1}^2>-{z_2}^2$ | |
| B. | $|{{z_1}-{z_2}}|=\sqrt{{z_1}^2+{z_2}^2-4{z_1}{z_2}}$ | |
| C. | ${z_1}^2+{z_2}^2=0?{z_1}={z_2}$ | |
| D. | |z1|2=|$\overline{{z}_{1}}$|2 |
3.设$\overrightarrow a$,$\overrightarrow b$是两个不共线向量,且向量$\overrightarrow a+λ\overrightarrow b$与$-\overrightarrow b+2\overrightarrow a$共线,则λ=( )
| A. | 0 | B. | $-\frac{1}{2}$ | C. | -2 | D. | $\frac{1}{2}$ |
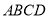 所在的平面与△
所在的平面与△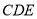 所在的平面交于
所在的平面交于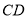 ,
,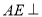 平面
平面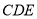 ,且
,且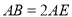 .
.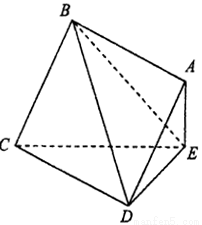
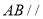 平面
平面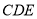 ;
;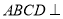 平面
平面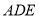 .
.