题目内容
4.已知直线Ax+By+C=0,设P(x0,y0)为直线Ax+By+C=0上一点,证明:这条直线的方程可以写成A(x-x0)+B(y-y0)=0.
分析 点是直线上的点,则点的坐标满足直线的方程,把点的坐标代入直线的方程,整理成所要的形式
解答 证明∵P(x0,y0)在直线Ax+By+C=0上,
∴(x0,y0)满足方程Ax+By+C=0,即Ax0+By0+C=0,
∴C=-Ax0-By0,
故Ax+By+C=0可化为Ax+By-Ax0-By0=0,
即A(x-x0)+B(y-y0)=0
点评 本题考查了直线方程的形式,属于基础题

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
18.已知集合A={1,2,5},N={x|x≤2},则M∩N等于( )
| A. | {1} | B. | {5} | C. | {1,2} | D. | {2,5} |
13.已知点A(2,-3),B(-3,-2),直线m过P(1,1),且与线段AB相交,求直线m的斜率k的取值范围为( )
| A. | $k≥\frac{3}{4}或k≤-4$ | B. | $k≥\frac{3}{4}或k≤-\frac{1}{4}$ | C. | -4≤k≤$\frac{3}{4}$ | D. | $\frac{3}{4}$≤k≤4 |
8.已知AD与BC是四面体ABCD中相互垂直的棱,若AD=BC=6,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是( )
| A. | $18\sqrt{2}$ | B. | $36\sqrt{2}$ | C. | 18 | D. | 36 |
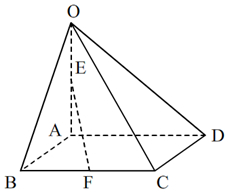 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点, 的解集为 .
的解集为 .