题目内容
7.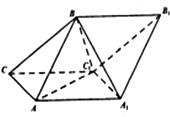 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.(I) 求证:AA1⊥BC1;
(Ⅱ)求三棱锥A1-ABC1的体积.
分析 (Ⅰ)取AA1的中点D,连结DB、DC1,推导出AA1⊥BD,AA1⊥C1D,由此能证明AA1⊥BC1.
(Ⅱ)三棱锥A1-ABC1的体积:${V}_{{A}_{1}-AB{C}_{1}={V}_{B-A{A}_{1}{C}_{1}}}$,由此能求出结果.
解答 证明:(Ⅰ)∵斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,A1B=AB=AA1=2,
∴A1A=A1C1=CC1=CA=2,△AA1B是等边三角形,
取AA1的中点D,连结DB、DC1,则AA1⊥BD,
由${S}_{△A{A}_{1}{C}_{1}}$=$\frac{1}{2}×{A}_{1}A×{A}_{1}{C}_{1}×sin∠A{A}_{1}{C}_{1}$=2sin∠AA1C1=$\sqrt{3}$,
得sin∠AA1C1=$\frac{\sqrt{3}}{2}$,
又∠AA1C1为锐角,∴∠AA1C1=60°,
∴△AA1C1是等边三角形,且AA1⊥C1D,
又∵BD?平面BC1D,C1D?平面BC1D,BD∩C1D=D,
∴AA1⊥平面BC1D,
∵BC1?平面BC1D,∴AA1⊥BC1.
解:(Ⅱ)由(Ⅰ)知BD⊥AA1,又侧面ABB1A1⊥侧面AA1C1C,
侧面ABB1A1∩侧面AA1C1C=AA1,
BD?平面ABB1A1,∴BD⊥平面ABB1A1,
在△AA1B中,A1B=AB=AA1=2,∴BD=$\sqrt{3}$,
∴三棱锥A1-ABC1的体积:
${V}_{{A}_{1}-AB{C}_{1}={V}_{B-A{A}_{1}{C}_{1}}}$=$\frac{1}{3}×\sqrt{3}×\sqrt{3}=1$.
点评 本题考查异面直线垂直的证明,考查三棱锥的体积的求法,是中档题,注意空间思维能力的培养.

 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
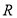 上的函数
上的函数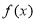 满足:
满足: 的图象关于
的图象关于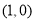 点对称,且当
点对称,且当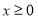 时恒有
时恒有 ,当
,当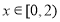 时,
时,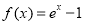 ,则
,则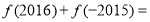 ( )
( )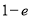 B.
B.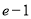
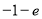 D.
D.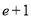
 的前
的前 项和
项和 ,若
,若 ,且
,且 ,则
,则 等于( )
等于( ) B.
B.
 D.
D.