题目内容
12.某几何体三视图如图所示,则这个几何体的体积为$\frac{4\sqrt{3}}{3}$,外接球的体积为$\frac{28\sqrt{21}}{27}$π.
分析 首先由几何体的三视图还原几何体,然后求体积.其外接球,与以俯视图为底面,以4为高的直三棱柱的外接球相同,进而可得该几何体外接球的体积.
解答 解:由已知三视图得该几何体是以底面边长为2的正方形,高为$\sqrt{3}$的四棱锥,
所以其体积为$\frac{1}{3}×{2}^{2}×\sqrt{3}$=$\frac{4\sqrt{3}}{3}$;
其外接球,与以俯视图为底面,以2为高的直三棱柱的外接球相同,
如图所示:
由题意可得底面外接圆的半径为:r=$\frac{2\sqrt{3}}{3}$,
由棱柱高为2,可得球心距为1,
故外接球半径为:R=$\sqrt{\frac{4}{3}+1}$=$\sqrt{\frac{7}{3}}$,
故外接球的体积V=$\frac{4}{3}$πR3=$\frac{28\sqrt{21}}{27}$π.
故答案为$\frac{4\sqrt{3}}{3}$;$\frac{28\sqrt{21}}{27}$π.
点评 本题考查的知识要点:三视图和立体图之间的转换,几何体的体积公式的应用,主要考查学生的空间想象能力和应用能力.

练习册系列答案
相关题目
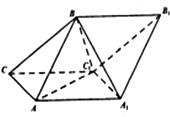 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角. .
.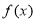 在
在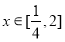 内单调递减,求实数
内单调递减,求实数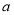 的取值范围;
的取值范围;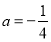 时,关于
时,关于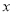 的方程
的方程 在
在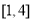 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数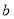 的取值范围.
的取值范围. 的图象经过点
的图象经过点 ,则
,则 ( )
( ) 与向量
与向量 平行,则
平行,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.