Question

【题目】已知f(x)＝xln x，g(x)＝x3＋ax2－x＋2.

(1)如果函数g(x)在区间上单调递减，求实数a的取值范围；

(2)对任意x∈(0，＋∞)，2f(x)≤g′(x)＋2恒成立，求实数a的取值范围．

Answer 1

【答案】(1)(2) [－2，＋∞)

【解析】

（1）转化为导函数在在区间上恒非正，再根据二次函数性质列式求解，（2）先化简不等式并变量分离，再利用导数研究新函数单调性以及最值，即得结果.

解：(1)

由题意，对恒成立，

则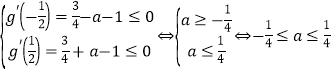

(2)由题意在上恒成立，

可得，设

则＝－＋＝－ ，

令＝0，得x＝1或－(舍)，

当0＜x＜1时，＞0，当x＞1时，＜0，

所以当x＝1时，取得最大值，＝－2

所以≥－2，所以的取值范围是[－2，＋∞).