Question

【题目】已知椭圆E：的右焦点为，离心率为，过作与x轴垂直的直线与椭圆交于P，Q点，若|PQ|=．

（1）求椭圆E的方程；

（2）设过的直线l的斜率存在且不为0，直线l交椭圆于A，B两点，若以AB为直径的圆过椭圆左焦点，求直线l的方程．

Answer 1

【答案】（1）（2）

【解析】

（1）由，①，，②，又，③，解得即可.

（2）设A，B，直线l的方程为x=my+2，代入椭圆方程可得，根据韦达定理和向量的运算即可求出m的值，可得直线方程.

（1）由，①，

∵过作与x轴垂直的直线与椭圆交于P、Q两点，|PQ|=

∴②

又③，

由①②③解得，，c=2，

∴椭圆方程为

（2）设A，B，

直线l的方程为x=my+2，代入椭圆方程可得，

∴，

∵F（-2，0），

∴，，

∵以AB为直径的圆过椭圆左焦点，

∴，

∴

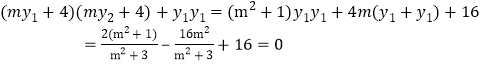
解得=23，即

故直线l的方程为