题目内容
3.若sin($\frac{π}{3}$-α)=$\frac{3}{5}$,则sin($\frac{π}{6}$-2α)=$-\frac{7}{25}$.分析 运用角的等价变化得到sin($\frac{π}{3}$-α)=$\frac{3}{5}$=sin($\frac{π}{2}-\frac{π}{6}$-α)=cos($\frac{π}{6}+α$),运用倍角公式求值.
解答 解:因为sin($\frac{π}{3}$-α)=$\frac{3}{5}$=sin($\frac{π}{2}-\frac{π}{6}$-α)=cos($\frac{π}{6}+α$),
则sin($\frac{π}{6}$-2α)=sin($\frac{π}{2}-\frac{π}{3}$-2α)=cos($\frac{π}{3}+2α$)=cos2($\frac{π}{6}+α$)=2cos2($\frac{π}{6}+α$)-1=-$\frac{7}{25}$;
故答案为:-$\frac{7}{25}$.
点评 本题考查了三角函数式的化简求值;灵活对角进行等价变化,运用倍角公式求值是关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
14.已知集合A={1,2,3,4,5},B={3,4,5,6,7},则图中阴影部分表示的集合为( )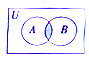

| A. | {1,2,3,4,5} | B. | {3,4,5,6,7} | C. | {1,2,3,4,5,6,7} | D. | {3,4,5} |
11.已知直线l1:(m-4)x-(2m+4)y+2m-4=0与l2:(m-1)x+(m+2)y+1=0,则“m=-2”是“l1∥l2”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分又不必要 |
18.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点为F1、F2,在双曲线上存在点P满足3|$\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}|≤2|\overrightarrow{{F_1}{F_2}}$|,则双曲线的渐近线的斜率$\frac{b}{a}$的取值范围是( )
| A. | $0<\frac{b}{a}≤\frac{3}{2}$ | B. | $\frac{b}{a}≥\frac{3}{2}$ | C. | $0<\frac{b}{a}≤\frac{{\sqrt{5}}}{2}$ | D. | $\frac{b}{a}≥\frac{{\sqrt{5}}}{2}$ |
8.函数y=$\frac{lg|x|}{x}$的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=λ|PF2|(λ>1),$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,双曲线的离心率为$\sqrt{2}$,则λ=( )
| A. | $\sqrt{2}$ | B. | $2+\sqrt{3}$ | C. | $2+\sqrt{2}$ | D. | $2\sqrt{3}$ |
12.已知集合A={x|x2-4x≤0,x∈Z},B={y|y=m2,m∈A},则A∩B=( )
| A. | {0,1,4} | B. | {0,1,6} | C. | {0,2,4} | D. | {0,4,16} |
 如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.
如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.