题目内容
4.已知定义在R内的奇函数f(x)满足:对任意x∈R郡有f(x+1)=f(3-x),若f(1)=-2,则2016f(2016)-2015f(2015)=( )| A. | -2015 | B. | 2015 | C. | -4030 | D. | 4030 |
分析 根据函数的奇偶性和对称的关系求出函数的周期是8,利用函数奇偶性和周期性将函数进行转化求解即可.
解答 解:定义在R内的奇函数f(x)满足:对任意x∈R郡有f(x+1)=f(3-x),
则f(x+1)=f(3-x)=-f(x-3),
则f(x+4)=-f(x),
即f(x+8)=-f(x+4)=f(x),
即函数f(x)是周期为8的周期函数,
则f(2016)=f(252×8)=f(0)=0,
f(2015)=f(252×8-1)=f(-1)=-f(1)=2,
故2016f(2016)-2015f(2015)=0-2015×2=-4030,
故选:C.
点评 本题主要考查函数值的计算,根据条件得到函数的周期性以及利用周期性和奇偶性的关系进行转化是解决本题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
12.若函数f(x)=b+lg($\sqrt{{x}^{2}+1}$-ax)是定义在R上的奇函数,则a+b=( )
| A. | -1 | B. | 0 | C. | -1或1 | D. | 0或2 |
16.若sinα=$\frac{1}{\sqrt{5}}$,sinβ=$\frac{1}{\sqrt{10}}$,且α、β∈(0,$\frac{π}{2}$),则α+β是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{3}$ |
14.下列式子正确的是( )
| A. | cos(-$\frac{π}{10}$)<cos(-$\frac{π}{9}$) | B. | tan$\frac{π}{6}$<tan$\frac{2}{7}$π | C. | sin$\frac{8}{7}$π>sin$\frac{π}{11}$ | D. | cos$\frac{2}{5}$π<cos$\frac{6}{5}$π |
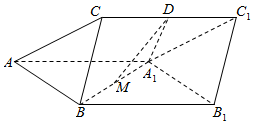 如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.