题目内容
7.已知椭圆C的中心在原点,离心率为$\frac{{\sqrt{3}}}{2}$,且与抛物线${y^2}=4\sqrt{3}x$有共同的焦点.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设椭圆C的左、右顶点分别为A1、A2,P为椭圆C上异于A1、A2的动点,直线A1P、A2P分别交直线l:x=4于M、N两点,设d为M、N两点之间的距离,求d的最小值.
分析 (I)抛物线${y^2}=4\sqrt{3}x$的焦点为$(\sqrt{3},0)$,即为椭圆的焦点.设椭圆C的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).由题意可得:c=$\sqrt{3}$,$\frac{c}{a}=\frac{\sqrt{3}}{2}$,a2=b2+c2,联立解出即可得出.
(II)设P(x0,y0),(x0≠±2,y0≠0),可得$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,根据点斜式可得直线A1P、A2P的方程,分别交直线l:x=4于M,N两点,可得d=$\frac{1}{|\frac{{y}_{0}}{{x}_{0}-4}|}$,k=$\frac{{y}_{0}}{{x}_{0}-4}$表示经过椭圆上的点P(x0,y0)与点Q(4,0)的直线的斜率(y0≠0).设经过点Q且斜率为k的直线方程为:y=k(x-4),与椭圆方程联立,根据判别式即可得出.
解答 解:(I)抛物线${y^2}=4\sqrt{3}x$的焦点为$(\sqrt{3},0)$,即为椭圆的焦点.
设椭圆C的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
由题意可得:c=$\sqrt{3}$,$\frac{c}{a}=\frac{\sqrt{3}}{2}$,a2=b2+c2,
联立解得c=$\sqrt{3}$,a=2,b=1.
故椭圆C的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(II)由(I)可得:A1(-2,0),A2(2,0),设P(x0,y0),(x0≠±2,y0≠0),
则$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,∴$4{y}_{0}^{2}$=4-${x}_{0}^{2}$.
直线A1P、A2P的方程分别为:y=$\frac{{y}_{0}}{{x}_{0}+2}$(x+2),y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),分别交直线l:x=4于M$(4,\frac{6{y}_{0}}{{x}_{0}+2})$,N$(4,\frac{2{y}_{0}}{{x}_{0}-2})$两点,
d=$|\frac{6{y}_{0}}{{x}_{0}+2}-\frac{2{y}_{0}}{{x}_{0}-2}|$=$|\frac{4{y}_{0}{x}_{0}-16{y}_{0}}{{x}_{0}^{2}-4}|$=$|\frac{4{y}_{0}{x}_{0}-16{y}_{0}}{4{y}_{0}^{2}}|$=$|\frac{{x}_{0}-4}{{y}_{0}}|$=$\frac{1}{|\frac{{y}_{0}}{{x}_{0}-4}|}$,
k=$\frac{{y}_{0}}{{x}_{0}-4}$表示经过椭圆上的点P(x0,y0)与点Q(4,0)的直线的斜率(y0≠0).
设经过点Q且斜率为k的直线方程为:y=k(x-4),
联立$\left\{\begin{array}{l}{y=k(x-4)}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,化为:(1+4k2)x2-32k2x+64k2-4=0,
由△=(32k2)2-4(1+4k2)(64k2-4)≥0,化为:k2≤$\frac{1}{12}$,解得$-\frac{\sqrt{3}}{6}$≤k≤$\frac{\sqrt{3}}{6}$,k≠0,
∴k=±$\frac{\sqrt{3}}{6}$时,d取得最小值$\frac{1}{|±\frac{\sqrt{3}}{6}|}$=2$\sqrt{3}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、直线的方程、斜率计算公式,考查了推理能力与计算能力,属于难题.

 名校课堂系列答案
名校课堂系列答案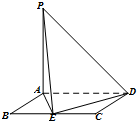 如图,已知四边形ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=4,E为BC的中点.
如图,已知四边形ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=4,E为BC的中点.