题目内容
17.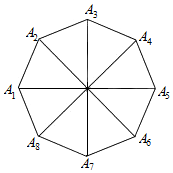 如图所示,中心为O的正八边形A1A2…A7A8中,$\overrightarrow{{a}_{i}}$=$\overrightarrow{{A}_{i}{A}_{i+1}}$(i=1,2,…,7),$\overrightarrow{{b}_{j}}$=$\overrightarrow{O{A}_{j}}$(j=1,2,…,8),试化简$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$.
如图所示,中心为O的正八边形A1A2…A7A8中,$\overrightarrow{{a}_{i}}$=$\overrightarrow{{A}_{i}{A}_{i+1}}$(i=1,2,…,7),$\overrightarrow{{b}_{j}}$=$\overrightarrow{O{A}_{j}}$(j=1,2,…,8),试化简$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$.
分析 根据向量的三角形法则和正八边形的性质化简.
解答 解:∵$\overrightarrow{{a}_{2}}$+$\overrightarrow{{b}_{7}}$=$\overrightarrow{{A}_{2}{A}_{3}}$+$\overrightarrow{O{A}_{7}}$=$\overrightarrow{{A}_{2}{A}_{3}}$+$\overrightarrow{{A}_{3}O}$=$\overrightarrow{{A}_{2}O}$,$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{5}}$=$\overrightarrow{{A}_{5}{A}_{6}}$+$\overrightarrow{O{A}_{5}}$=$\overrightarrow{O{A}_{6}}$=$\overrightarrow{{A}_{2}O}$,
∴$\overrightarrow{{a}_{2}}$+$\overrightarrow{{b}_{7}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{5}}$=$\overrightarrow{0}$,
∴$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$=$\overrightarrow{{b}_{2}}$.
点评 本题考查了平面向量运算的三角形法则,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7.某台小型晚会由6个不同的节目组成,演出顺序有如下要求:节目甲和节目乙排在一起,节目乙和节目丙不能排在一起,该台晚会节目演出顺序的编排方案有( )
| A. | 194种 | B. | 193种 | C. | 192种 | D. | 191种 |
8.若cosα+sinα=$\frac{2}{3}$,则$\frac{\sqrt{2}sin(2α-\frac{π}{4})+1}{1+tanα}$的值为( )
| A. | $\frac{5}{9}$ | B. | 0 | C. | -$\frac{5}{18}$ | D. | -$\frac{5}{9}$ |
12.对甲、乙两个班级的某次数学成绩进行统计,按照大于等于85分为优秀,85分以下为非优秀,得到如下所示的列联表:
已知在全部的105人中随机抽取1人,成绩优秀的概率为$\frac{2}{7}$.
(1)求b,c的值;
(2)根据表闻表中的数据,运用独立检验的思想方法分析:学生的数学成绩与班级是否有关系?并说明理由.
附:参考公式与临界值表:K2=$\frac{n(ab-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | b | |
| 乙班 | c | 30 | |
| 总计 | 105 |
(1)求b,c的值;
(2)根据表闻表中的数据,运用独立检验的思想方法分析:学生的数学成绩与班级是否有关系?并说明理由.
附:参考公式与临界值表:K2=$\frac{n(ab-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥K0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
2.设a>0,b>0,则“x>a且y>b”是“x+y>a+b,且xy>ab”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知关于某设备的使用年限x(年)和所支出的费用y(万元),有如表所示的统计资料:
根据上表提供的数据,求出了y关于x的线性回归方程为$\stackrel{∧}{y}$=1.23x+0.08,那么统计表中t的值为( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | t | 6.5 | 7.0 |
| A. | 5.5 | B. | 5.0 | C. | 4.5 | D. | 4.8 |
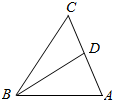 如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.
如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.