题目内容
7．某台小型晚会由6个不同的节目组成，演出顺序有如下要求：节目甲和节目乙排在一起，节目乙和节目丙不能排在一起，该台晚会节目演出顺序的编排方案有（ ）| A． | 194种 | B． | 193种 | C． | 192种 | D． | 191种 |
分析 利用间接法，求出节目甲和节目乙排在一起的所有的排列，再排除甲乙丙或丙乙甲在一起的种数，问题得以解决．
解答 解：节目甲和节目乙捆绑在一起看做一个复合元素，再和其它节目任意排有A22A55=240，
节目甲和节目乙和节目丙捆绑在一起看做一个复合元素（排成甲乙丙或丙乙甲的方式），再和其它节目任意排有A22A44=48，
则节目甲和节目乙排在一起，节目乙和节目丙不能排在一起，该台晚会节目演出顺序的编排方案240-48=192种，
故选：C，
点评 本题主要考查排列组合基础知识，考查分类与分步计数原理，利用间接法，属于基础题．
练习册系列答案
相关题目
15．已知随机变量ξ服从正态分布N（2，σ2），且函数f（x）=x2+2x-ξ+1不存在零点的概率为0.08，则随机变量P（0＜ξ＜2）=（ ）
| A． | 0.08 | B． | 0.42 | C． | 0.84 | D． | 0.16 |
12．设点A（3，3，1），B（1，0，5），C（0，1，0），则线段AB的中点与点C的距离为（ ）
| A． | $\frac{\sqrt{13}}{4}$ | B． | $\frac{\sqrt{13}}{2}$ | C． | $\frac{\sqrt{53}}{4}$ | D． | $\frac{\sqrt{53}}{2}$ |
16．若函数y=f（x）的图象上存在关于原点对称的两点M，N，则称函数f（x）有一组“对点”（“M与N”和“N与M”视为同一组“对点”），已知f（x）=$\left\{\begin{array}{l}{2x^2+4x，x＜0}\\{\frac{m}{e^x}，x≥0}\end{array}\right.$，有两组“对点”，则非零实数m的取值范围是（ ）
| A． | （（4-4$\sqrt{2}$）•e${\;}^{-\sqrt{2}}$，0）∪（0，（4$\sqrt{2}$-4）•e${\;}^\sqrt{2}$） | B． | （（2-2$\sqrt{2}$）•e${\;}^{-\sqrt{2}}$，0）∪（0，（2$\sqrt{2}$-2）•e${\;}^\sqrt{2}$） | ||
| C． | （0，（2$\sqrt{2}$-2）•e${\;}^\sqrt{2}$） | D． | （0，（4$\sqrt{2}$-4）•e${\;}^\sqrt{2}$） |
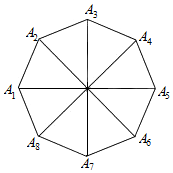如图所示，中心为O的正八边形A1A2…A7A8中，$\overrightarrow{{a}_{i}}$=$\overrightarrow{{A}_{i}{A}_{i+1}}$（i=1，2，…，7），$\overrightarrow{{b}_{j}}$=$\overrightarrow{O{A}_{j}}$（j=1，2，…，8），试化简$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$．