题目内容
8．若cosα+sinα=$\frac{2}{3}$，则$\frac{\sqrt{2}sin（2α-\frac{π}{4}）+1}{1+tanα}$的值为（ ）| A． | $\frac{5}{9}$ | B． | 0 | C． | -$\frac{5}{18}$ | D． | -$\frac{5}{9}$ |
分析 由cosα+sinα=$\frac{2}{3}$，两边平方可得：2sinαcosα=-$\frac{5}{9}$．再利用和差公式、同角三角函数基本关系式即可得出$\frac{\sqrt{2}sin（2α-\frac{π}{4}）+1}{1+tanα}$．
解答 解：∵cosα+sinα=$\frac{2}{3}$，∴1+2sinαcosα=$\frac{4}{9}$，∴2sinαcosα=-$\frac{5}{9}$．
∴$\frac{\sqrt{2}sin（2α-\frac{π}{4}）+1}{1+tanα}$=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}（sin2α-cos2α）+1}{1+tanα}$=$\frac{2sinαcosα+2si{n}^{2}α}{1+\frac{sinα}{cosα}}$=2sinαcosα=-$\frac{5}{9}$．
故选：D．
点评 本题考查了和差公式、同角三角函数基本关系式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
16．若函数y=f（x）的图象上存在关于原点对称的两点M，N，则称函数f（x）有一组“对点”（“M与N”和“N与M”视为同一组“对点”），已知f（x）=$\left\{\begin{array}{l}{2x^2+4x，x＜0}\\{\frac{m}{e^x}，x≥0}\end{array}\right.$，有两组“对点”，则非零实数m的取值范围是（ ）
| A． | （（4-4$\sqrt{2}$）•e${\;}^{-\sqrt{2}}$，0）∪（0，（4$\sqrt{2}$-4）•e${\;}^\sqrt{2}$） | B． | （（2-2$\sqrt{2}$）•e${\;}^{-\sqrt{2}}$，0）∪（0，（2$\sqrt{2}$-2）•e${\;}^\sqrt{2}$） | ||
| C． | （0，（2$\sqrt{2}$-2）•e${\;}^\sqrt{2}$） | D． | （0，（4$\sqrt{2}$-4）•e${\;}^\sqrt{2}$） |
3．若函数f（x）的定义域为[2，4]，则函数y=f（log${\;}_{\frac{1}{2}}$x）的定义域为（ ）
| A． | [$\frac{1}{2}$，1] | B． | [4，16] | C． | [2，4] | D． | [$\frac{1}{16}$，$\frac{1}{4}$] |
13．已知集合A={x|x2-2x-3=0}，B={x|-2＜x＜3}，则A∩B=（ ）
| A． | {-1，3} | B． | {-1} | C． | {3} | D． | ∅ |
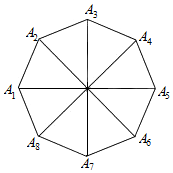如图所示，中心为O的正八边形A1A2…A7A8中，$\overrightarrow{{a}_{i}}$=$\overrightarrow{{A}_{i}{A}_{i+1}}$（i=1，2，…，7），$\overrightarrow{{b}_{j}}$=$\overrightarrow{O{A}_{j}}$（j=1，2，…，8），试化简$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$．