题目内容

16．已知集合A={x|x≤4}，B={x|x2＞4}，则A∩B=（　　）
A．{x|-2＜x＜2}B．{x|x＜-2或x＞2}C．{x|x＜-2或2＜x≤4}D．{x|x＜-2或2＜x＜4}

分析 根据题意，解x2＞4可得集合B，进而由交集的定义计算可得答案．

解答 解：根据题意，x2＞4⇒x＜-2或x＞2，
即B={x|x2＞4}={x|x＜-2或x＞2}，
则A∩B={x|x＜-2或2＜x≤4}，
故选：C．

点评 本题考查集合交集的计算，关键是正确表示出集合B．

练习册系列答案
相关题目
6．设F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，双曲线上存在一点P使得∠F1PF2=60°，|OP|=3b（O为坐标原点），则该双曲线的离心率为（　　）
A．$\frac{4}{3}$B．$\frac{2\sqrt{3}}{3}$C．$\frac{7}{6}$D．$\frac{\sqrt{42}}{6}$
7．若x，y满足约束条件$\left\{\begin{array}{l}{x＜2}\\{x+y-2≥0}\\{x-y+2≥0}\end{array}\right.$，则$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{2}$．
4．函数f（x）=sin（πx+θ）（|θ|＜$\frac{π}{2}$）的部分图象如图，且f（0）=-$\frac{1}{2}$，则图中m的值为（　　）
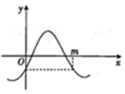
A．1B．$\frac{4}{3}$C．2D．$\frac{4}{3}$或2
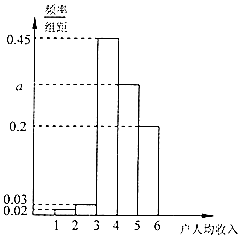11．我国为确保贫困人口到2020年如期脱贫，把2017年列为“精准扶贫”攻坚年，2017年1月1日某贫困县随机抽取100户贫困家庭的每户人均收入数据做为样本，以考核该县2016年的“精准扶贫”成效（2016年贫困家庭脱贫的标准为人均收入不小于3000元）．根据所得数据将人均收入（单位：千元）分成五个组：[1，2），[2，3），[3，4），[4，5），[5，6]，并绘制成如图所示的频率分布直方图．
（1）求频率分布直方图中a的值；
（2）如果被抽取的100户贫困家庭有80%脱贫，则认为该县“精准扶贫”的成效是理想的．请从统计学的角度说明该县的“精准扶贫”效果是理想还是不理想？
（3）从户人均收入小于3千元的贫困家庭中随机抽取2户，求至少有1户人均收入在区间[1，2）上的概率．
1．已知函数f（x）=2sinωx-4sin2$\frac{ωx}{2}$+2+m（其中ω＞0，m∈R），且当x=$\frac{1}{2}$时，f（x）的图象在y轴右侧得到第一个最高点．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）若f（x）在区间[2，4]上的最大值为5，最小值是p，求m和p的值．
8．已知焦点在x轴上，离心率为$\frac{{\sqrt{6}}}{3}$的椭圆C的一个顶点是（0，1）．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设直线l与椭圆C交于A、B两点，且OA⊥OB，O为坐标原点，判断直线l与圆x2+y2=1的位置关系？证明你的结论．
11．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知atanB=2bsinA．
（1）求B；
（2）若b=$\sqrt{3}$，A=$\frac{5π}{12}$，求△ABC的面积．
12．“x＜3”是“ln（x-2）＜0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网