题目内容
6.椭圆两焦点为F1(-4,0),F2(4,0),P在椭圆上,若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,△PF1F2的面积为9,则该椭圆的标准方程为( )| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{4}$=1 |
分析 根据题意,分析可得2c=|F1F2|=8,以及PF1⊥PF2,即△PF1F2的为直角三角形,又由△PF1F2的面积为9,分析可得|PF1|•|PF2|=18,结合勾股定理分析可得(|PF1|+|PF2|)2=|PF1|2+|PF2|2+2|PF1|•|PF2|=100,变形可得2a=|PF1|+|PF2|=10,即a=5,计算可得b的值,将a、b的值代入椭圆的标准方程,计算可得答案.
解答 解:根据题意,椭圆两焦点为F1(-4,0),F2(4,0),
则有2c=|F1F2|=8,即c=4,
又由$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,则PF1⊥PF2,即△PF1F2的为直角三角形,
又由△PF1F2的面积为9,则有$\frac{1}{2}$(|PF1|•|PF2|)=9,即|PF1|•|PF2|=18;
又由|F1F2|=8,即|PF1|2+|PF2|2=|F1F2|2=64;
则(|PF1|+|PF2|)2=|PF1|2+|PF2|2+2|PF1|•|PF2|=100,
即2a=|PF1|+|PF2|=10,则a=5,
又由c=4,则b2=a2-c2=9;
故椭圆的标准方程为:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1;
故选:A.
点评 本题考查椭圆的几何性质,关键是求出|PF1|+|PF2|的值.

练习册系列答案
相关题目
10.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期是π,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度后得到函数图象过点P(0,1),则函数f(x)=sin(ωx+φ)( )
| A. | 有一个对称中心($\frac{π}{12}$,0) | B. | 有一条对称轴x=$\frac{π}{6}$ | ||
| C. | 在区间[-$\frac{π}{12}$,$\frac{5π}{12}$]上单调递减 | D. | 在区间[-$\frac{π}{12}$,$\frac{5π}{12}$]上单调递增 |
18.已知圆O:x2+y2=1,点P为直线x-2y-3=0上一动点,过点P向圆O引两条切线PA,PB,A、B为切点,则直线AB经过定点( )
| A. | (2,0) | B. | (3,0) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{3}$,-$\frac{2}{3}$) |
15.复数z=(a2-1)+(a-1)i(a∈R)为纯虚数,则z=( )
| A. | i | B. | -2i | C. | 2i | D. | -i |
16.上世纪八十年代初,邓小平同志曾指出“在人才的问题上,要特别强调一下,必须打破常规去发现、选拔和培养杰出的人才”.据此,经省教育厅批准,某中学领导审时度势,果断作出于1985年开始施行超常实验班教学试验的决定.一时间,学生兴奋,教师欣喜,家长欢呼,社会热议.该中学实验班一路走来,可谓风光无限,硕果累累,尤其值得一提的是,1990年,全国共招收150名少年大学生,该中学就有19名实验班学生被录取,占全国的十分之一,轰动海内外.设该中学超常实验班学生第x年被录取少年大学生的人数为y.
(1)左下表为该中学连续5年实验班学生被录取少年大学生人数,求y关于x的线性回归方程,并估计第6年该中学超常实验班学生被录取少年大学生人数;
附1:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline y$-$\stackrel{∧}{b}$$\overline{x}$
(2)如表是从该校已经毕业的100名高中生录取少年大学生人数与是否接受超常实验班教育得到2×2列联表,完成上表,并回答:是否有95%以上的把握认为“录取少年大学生人数与是否接受超常实验班教育有关系”.
附2:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
(1)左下表为该中学连续5年实验班学生被录取少年大学生人数,求y关于x的线性回归方程,并估计第6年该中学超常实验班学生被录取少年大学生人数;
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 录取人数y | 10 | 11 | 14 | 16 | 19 |
(2)如表是从该校已经毕业的100名高中生录取少年大学生人数与是否接受超常实验班教育得到2×2列联表,完成上表,并回答:是否有95%以上的把握认为“录取少年大学生人数与是否接受超常实验班教育有关系”.
附2:
| 接受超常实验班教育 | 未接受超常实验班教育 | 合计 | |
| 录取少年大学生 | 60 | 20 | 80 |
| 未录取少年大学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| P(k2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 |
| k0 | 0.455 | 0.708 | 2.706 | 3.841 |
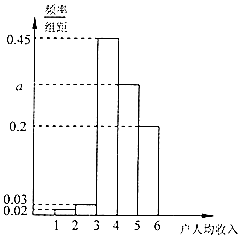 我国为确保贫困人口到2020年如期脱贫,把2017年列为“精准扶贫”攻坚年,2017年1月1日某贫困县随机抽取100户贫困家庭的每户人均收入数据做为样本,以考核该县2016年的“精准扶贫”成效(2016年贫困家庭脱贫的标准为人均收入不小于3000元).根据所得数据将人均收入(单位:千元)分成五个组:[1,2),[2,3),[3,4),[4,5),[5,6],并绘制成如图所示的频率分布直方图.
我国为确保贫困人口到2020年如期脱贫,把2017年列为“精准扶贫”攻坚年,2017年1月1日某贫困县随机抽取100户贫困家庭的每户人均收入数据做为样本,以考核该县2016年的“精准扶贫”成效(2016年贫困家庭脱贫的标准为人均收入不小于3000元).根据所得数据将人均收入(单位:千元)分成五个组:[1,2),[2,3),[3,4),[4,5),[5,6],并绘制成如图所示的频率分布直方图.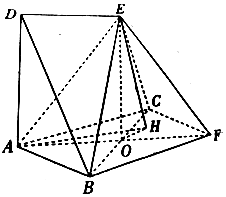 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°