题目内容
17.在△ABC中,BC=2,AC=1,以AB为边作等边三角形ABD(C,D两点在直线AB的两侧),当∠C变化时,线段CD长的最大值为3,此时C=120°.分析 通过旋转三角形将长度等于CD,AC,BC的三条边转化到同一个三角形当中,使用余弦定理求出CD的最值.
解答 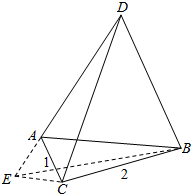 解:如图,△ABD是等边三角形,将△ACD绕A逆时针旋转60°得到△AEB,
解:如图,△ABD是等边三角形,将△ACD绕A逆时针旋转60°得到△AEB,
则AC=AE=1,∠CAE=60°,CD=BE,∴△ACE是等边三角形,∴CE=1,∠ACE=60°.
在△BCE中,∠BCE=∠ACB+60°,CE=1,BC=2,∴BE=$\sqrt{{2}^{2}+{1}^{2}-4cos(∠ACB+60°)}$.
∴当cos(∠ACB+60°)=-1即∠ACB=120°时BE取得最大值3.即CD的最大值是3.
故答案为3,120°.
点评 本题考查了余弦定理得应用,对三角形进行旋转,将边长为1,2,CD的线段转化到同一个三角形中是解题关键.

练习册系列答案
相关题目
7.不等式x2+2x-3≤0的解集为( )
| A. | [-1,3] | B. | [-3,-1] | C. | [-3,1] | D. | [1,3] |
8.设函数f(x)=sin2x+$\sqrt{3}cos2x$+$\frac{π}{6}$的图象关于点(x0,y0)成中心对称,且x0$∈(\frac{π}{2},π)$,则x0+y0=( )
| A. | π | B. | $\frac{π}{2}$ | C. | $π或\frac{π}{2}$ | D. | 0或$\frac{π}{2}$ |
5.“直线ax+3y+1=0与直线2x+(a+1)y+1=0平行”是“a=-3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+y≤3}\\{x+y≥2}\\{x≥0,y≥0}\end{array}\right.$,若z=-2x-y,则z的最小值为( )
| A. | -3 | B. | 3 | C. | -4 | D. | -6 |
2.设P为△ABC内部及边界上一点,当|PA|+|PB|+|PC|取得最大值时,P点( )
| A. | 在△ABC的内部(不含边界) | B. | 在△ABC的边界上(不含顶点) | ||
| C. | 为△ABC的某个定点 | D. | 以上都有可能,视△ABC的形状而定 |